Moment of Inertia of Cylinder About Perpendicular Axis

Before learning the derivation of the moment of inertia of a cylinder about a perpendicular axis we must thoughtfully understand what is a moment of inertia. The moment of inertia is an opposing force experienced by any object or entity when it is rotated about an axis. The axis of rotation can be any axis, it can be either the axis of the entity as well as it can be far away from the entity’s axis. 

Speaking about the moment of inertia of a cylinder’s derivation. To derive it we can easily cut a large cylinder of length l into small elemental disks and we can find the moment of inertia of that small disk. And after that, we can easily integrate the MOI of the disk having a limitation of the length of the cylinder to find the moment of inertia of the complete cylinder.

Let us initially have a look at the moment of inertia of a cylinder about a perpendicular axis passing through its centre for a better understanding,

I = ¼(MR²) + 1/12 (ML²)

Where,

M is the cylinder’s mass,

R is the cylinder’s radius 

And L is the cylinder’s length.

Before proceeding further, let us also have a look at the moment of inertia of a cylinder having its axis of rotation as its own axis.

I = ½MR²

Now, we are going to derive the formula step by step using the method stated in para 2. 

Derivation

To begin with, we must first draw the diagram and understand all the annotations.

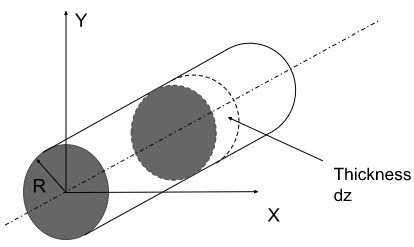
As in the diagram, consider the thickness of the elemental disk to be dz, the length of the cylinder to be L, the radius of the cylinder to be R and the mass of the cylinder to be M

Let us first find the mass of the small elemental disk, 

For that the density is given by,

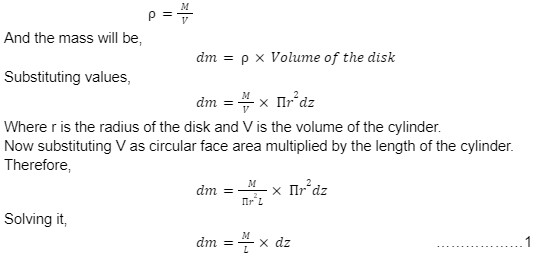
Here we got our moment of inertia of the disk about a perpendicular axis x. 

Now, to find the moment of inertia of the complete cylinder we are going to integrate equation 3 using the length of the cylinder as the limit which is from -L/2 to L/2.

Therefore, the equation becomes as,

Rewriting as,

                                              I = MR²/4 + ML²/12                       ………………..4

Here we go, equation 4 is the moment of inertia formula of a cylinder about the perpendicular axis. 

Conclusion

To sum up, the moment of inertia of a cylinder about a perpendicular axis can be found by dividing the whole cylinder into the form of small elemental disks. And finding the moment of inertia of that small elemental disk using the perpendicular axis theorem. After which, we can integrate the found moment of inertia of the disk to find out the moment of inertia of a complete cylinder about an axis perpendicular to it having limits from 0 to the length of the cylinder.