In material science, a moment of inertia is a quantifiable measurement of a body’s precise energy, the body’s protection from having its revolution speed about a hub changed by the arrangement of a force (turning force). The pivot may be interior or outside, and it tends to be fixed or not. The moment of inertia (I) is characterised as the amount of the items created by increasing the mass of every molecule of issue in a given article by the square of the separation from the hub concerning that hub.
Conservation of linear energy states that when a mass strikes an equivalent mass it remains very still and sticks to it, the mix should move at a large portion of the speed, on the grounds that the result of mass and speed should stay steady.
Utilising a string through a cylinder, a mass is moved in a level circle with rakish speed ω. Assuming the string is pulled down so the sweep is a large portion of the first range, then, at that point, protection of rakish energy directs that the ball should have multiple times the precise speed. This is on the grounds that the result of moment of inactivity and precise speed should stay consistent, and dividing the range lessens the moment of latency by an element of four.
With the proper equilibrium of power, a roundabout circle can be created by a power acting toward the middle. Acting opposite to the speed, it gives the fundamental centripetal power to keep it all around.
Assuming a turning haggle is upheld by one finish of the pivot, then, at that point, the force created by the heaviness of the haggle delivers a force that is opposite to the precise energy of the wheel. This shifts its course yet not its extent, making the tip of the hub follow out a circle. This is called precession, and is closely resembling the circle of a mass under a focal power.
ROTATIONAL INERTIA:
Rotational inertia is a property of any item which can be pivoted. It is a scalar value which lets us know that switching the rotational speed of the article up a given rotational axis is so troublesome.
Whenever a mass manoeuvres further from the line of axis of turn it turns out to be progressively more hard to change the rotational speed of the framework. Instinctively, this is on the grounds that the mass is currently hauling more energy with it around the circle (because of the greater speed) and in light of the fact that the force vector is changing all the more rapidly. Both of these impacts rely upon the separation from the axis.
. For a solitary body, for example, the cricket ball of mass m , turning at range of radius r from the pivot of revolution the rotational inactivity(inertia) is:
I=MR²
Further the S.I. units for Inertia is:
Kg*m
CALCULATION:
The moment of inertia (denoted as I) can be calculated by ;
I = L/ω
Here , ω symbolised the angular velocity and L symbolised the angular momentum.
Also,
I = ∑MR²
Here, M is the mass of the object and R is the
The following factors on which MOI depends:
- The mass of the body,
- Its shape and size distribution of mass on the rotation axes.
- The position and inclination on the axises.
MOMENT OF INERTIA OF A THIN ROD:
Consider a thin uniform rod of the mass M and length R about an axis perpendicular to the rod through its perpendicular bisector,
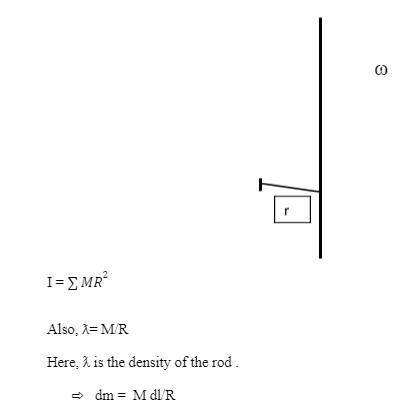
MOMENT OF INERTIA OF A NON- UNIFORM ROD:
Through the end
Consider a non uniform pole AB has mass M and Length 2R. The mass per unit length of the bar is mx at A place of the bar far off x from A.
The moment of inertia of the pole about a pivot opposite to the bar Through A will be,
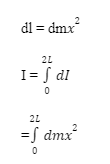

MOMENT OF INERTIA OF A UNIFORM THIN ROD:
The moment of inertia of a uniform thin rod about the axis passing through the centre is:
Let the mass be “M” and the length be “R”
The axis passing perpendicular at the distance of R/3 from one of the sides is: MR²/9
Derivation:
Distance of the point from the centre of the rod
=(R/2-R/3)
Applying parallel axis theorem
I =MR²12+M(R/2-R/3)
= MR²/12+MR²/36
=(3MR²+MR²)/36
=4MR²/36
=MR²/9
EXAMPLES OF MOMENT OF INERTIA:
FLYWHEEL of an auto: Flywheel is a weighty mass mounted on the driving rod of a motor. The extent of MOI of the flywheel is extremely high and helps in putting away the energy.
Anything you toss inside a vehicle will come down to you: Suppose you are on a bus. Then, at that point, you and every one of your assets move at a similar speed and have the latency of movement. So when you toss a ball upwards inside a bus, it ought to in a perfect world go in reverse yet because of the latency of movement, it will move with the speed of the bus. This illustration of idleness of movement is a piece hard to comprehend except if you attempt it in a moving vehicle.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out













