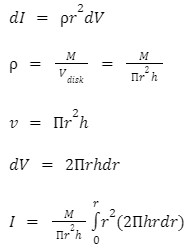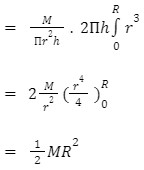Moment of Inertia of a Disk Derivation

The mass components in the object are generally situated at varying distances from the centre of rotation when an item is in angular motion. The total of the moments of inertia of the mass constituents in the object is the cumulative moment of inertia. In this article, we’ll look at the moment of inertia of a disk. A thin circular disc has the same moment of inertia as a solid cylinder of any length, but it requires special attention since it is frequently employed as an element in constructing the moment of inertia statement for other geometries, like the sphere or even the cylinder around an end diameter. The basic illustration of the perpendicular axis theorem is the moment of inertia around a diameter. 

Discover Unacademy UPSC Coaching Centres in the following locations 

• IAS Coaching in Mukherjee Nagar Delhi
• IAS Coaching in Karol Bagh
• UPSC Coaching in Prayagraj

Moment of Inertia

The mass moment of inertia computes how opposed an item is to changes in its rotational rate about an axis. The moment of inertia comes from Newton’s first law of motion, which deals with inertia.

Without pressures acting on them, objects at rest would oppose being propelled into motion, while objects in motion would resist stopping. The force required to move something in linear motion is equal to the product of its acceleration and mass (F=ma). 

To convert their movement from standing still to moving, higher masses demand more force. One of the numerous mass qualities that explain an object’s stability as well as the forces required to change its motion is the moment of inertia.

Circular disk

A thin circular disc has the same moment of inertia as a solid cylinder of any length, but it requires special attention since it is frequently employed as an element in constructing the moment of inertia statement for other geometries, like the sphere or even the cylinder around an end diameter. 

The basic illustration of the perpendicular axis theorem is the moment of inertia around a diameter. A spinning disc eventually comes to a halt, with a whirring sound of progressively greater frequency accompanying the last stage of motion. 

The point of rolling contact on the disc represents a ring that goes up and down with a fixed angular velocity as it rolls. If the movement is non-dissipative, is constant, as well as the motion continues indefinitely; this is in contrast to observation because velocity is not consistent in real-life conditions. 

Moment of inertia of a disk about an axis passing through its very centre as well as perpendicular to the plane

Assume a uniform circular disc with mass M & radius R that rotates along an axis z that passes through its centre.

The disc’s mass is equal to M.

The density is equal to

The disc’s radius is equal to R.

 Thus, the moment of inertia of a disc 

1. About an axis perpendicular to the disc 
2. Going through a point on the disk’s edge, of known Mass & radius R around any of its diameter

Is as follows: 

The disc’s moment of inertia as to its diameter is ¼ MR²

Utilising the perpendicular axes theorem,The disc’s moment of inertia around an axis travelling through its centre and perpendicular to the disc is equal to

 2 × ¼ MR² = ½ MR²

Using theorem axes, the disc’s moment of inertia while travelling through a location on its edge that is normal to the disc = ½ MR² +MR² = ¾ MR²

Conclusion

To summarize, mass moment of inertia measures how resistant an item is to changes in its rotational rate around an axis. The mass moment of inertia is from Newton’s first law of motion, which is about  with inertia. To convert their movement from standing still to moving, higher masses demand more force. A spinning disc eventually comes to a halt, with a whirring sound of progressively greater frequency accompanying the last stage of motion. Inertia is a linear mass attribute that describes how well an item opposes a change in movement. The mass moment of inertia of a disc about an axis passing through its very centre as well as perpendicular to the plane is ½ MR².