Moment Of Inertia Of A Circular Ring About Its Axis

Moment Of Inertia is the inherent quality of any object that signifies its tendency not to initiate any angular acceleration, or we can say oppose the rotational inertia if it is present at rest. 

Whenever the word, moment of inertia comes, you should understand immediately that there is one object that is either in a rotational motion around a fixed rotatory axis or an object is at a pure rest state, and it is forced to get into a rotational motion. 

 Just like Newton said in one of his laws of motion, “An object will only change its state of action if there is an external force applied to it.” Similar is the case of inertia in rotational motion. Inertia to avoid modification in an object’s actual state of action is called the Moment Of Inertia. In this article, we have collected the moment of inertia of a circular ring about its tangent, what will be the moment of inertia of a thin circular ring, and the overall moment of inertia for a circular ring.

Moment Of Inertia For A Circular Ring

After calculating the mass moment of inertia of a circular ring when the axis of rotation is passing from the center we can calculate the mass moment of inertia of the same circular ring from the axis of rotation placed in the plane of the ring like a diameter passing from the center by two theorems primarily known as perpendicular axis theorem and parallel axis theorem.

 To calculate the moment of inertia for a circular ring when the axis of rotation is a tangent we will have to take two-three steps to reach the proof of the above conditions. 

Moment Of Inertia For A Circular Ring From The Center and Perpendicular To The Plane

 Let the total mass of the circular ring be equal to M and the radius from the center to the perimeter is R.

 We will take an elementary unit section from the perimeter of the ring to calculate the moment of inertia of that elementary section and proceed further by integrating that into the complete ring because a ring is a symmetrical mass distribution body.

 dm = (M / 2πR) …………(i)

 We know the formula for the moment of inertia for the elementary ring section.

 dI = dm(R2)  ……………..(ii)

 Replacing dm from equation (i) and putting it in equation (ii).

 dI = (M/2πR)(R)2

 Now, integrating the mass moment of inertia calculated for the elementary section to the whole perimeter of the circular ring to calculate the moment of inertia of a thin circular ring.

 ∫dI = ∫(M/2πR)(R)2 . dx

 Taking the constant parameters out from the integration such as the complete mass M, the total radius R, and the two pi(2π).

 I = (RM/ 2π) o∫2πR dx

 Because, [Integration of ∫dx = x]

 Hence, I = (M / 2π) . [x]02πR

 Solving further by putting the upper limit in the equation first and then subtracting the value obtained by putting the lower limit in the equation.

 I = (RM/2π)  [2πR – 0]

 I = MR2

 Therefore, the mass moment of inertia of a thin circular ring is I = MR2.

Moment Of Inertia Of A Circular Ring About Its Diameter

To find out the value of the moment of inertia of a circular ring about its tangent, we will first have to calculate the theoretical value of the moment of inertia of a thin circular ring from the axis of diameter.

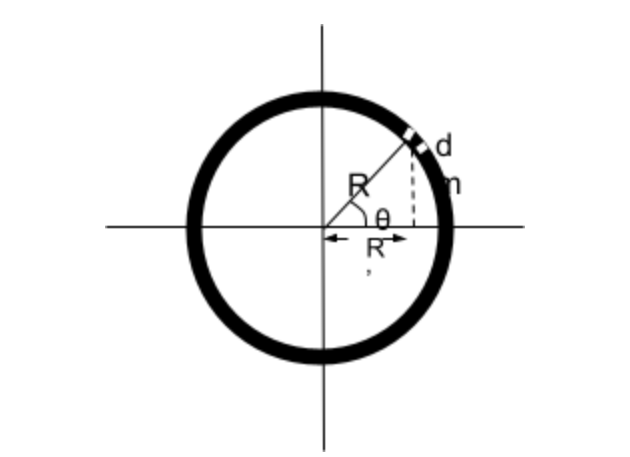
 Let the total mass of the circular ring be equal to M and the radius from the center to the perimeter is R.

 We will take an elementary unit section from the perimeter of the ring to calculate the moment of inertia of that elementary section and proceed further by integrating that into the complete ring because a ring is a symmetrical mass distribution body.

 I = ∫dm.R’2

 dm = M / 2π.dθ ……………….(i)

 R’ = Rcosθ

 Now, integrating the mass moment of inertia calculated for the elementary section to the whole perimeter of the circular ring to calculate the moment of inertia of a thin circular ring.

 I = o∫2π R2 cos2θ . (M / 2π) dθ

 Taking the constant parameters out from the integration such as the complete mass M, the total radius R, and the two pi(2π).

 I = R2M / 2πo∫2π cos2θ.dθ

 I = R2M/2π[θ/2 + (sin 2θ) / 4]o2π……………[ Because, ∫cos2θ.dθ = θ / 2 + (sin 2θ) / 4 + C]

 I = R2M / 2π[( π + 0) – (0 + 0)]

 I = MR2 /2

Moment Of Inertia Of A Circular Ring About Its Tangent

By applying the perpendicular axis theorem on the results of mass moment of inertia obtained above. We can calculate the mass moment about the tangent.

 The moment of inertia of a circular ring about its tangent, I’ = I + MR2 

 I’ = MR2/2 + MR2 = 3MR2/2 = 3I

 I = 3MR2/2

Conclusion

A circular ring is a type of solid that has continuous mass distribution throughout its body.  The moment of inertia of a circular ring about its tangent can be calculated with great ease if we focus on deriving the mass moment of inertia for a similar circular ring but this time the axis of rotation is not a tangent to the ring but a straight line of an axis passing from the center of the ring in the direction perpendicular to the plane of the ring.