Moment of Inertia Formula

Suppose a body is unrestricted to rotate around its axis. So, what should we do to make an object undergo angular momentum? It is the force of torque that makes an object rotate. In general words, torque can be defined as the estimate of the force that can result in an object revolving about an axis. Just as a force is what induces an object to accelerate from its original position, the activity of torque does the same for rotational movements. So, the amount of torque that is needed by the body to undergo rotational movement is proportional to the moment of inertia that is present in the body. The concept of moment of inertia depends upon various factors and has a major role in the area of rotational kinematics. 

What is a Moment of Inertia?

Moment of Inertia can be described as the amount or the quantity which is required to decide the amount of torque needed, to make the body go in angular acceleration around the rotational axis. It is also known by terms like angular mass, rotational inertia, mass moment of inertia and second moment of mass. Generally, we can define this concept as the multitude which specifies the amount of torque that is needed to put a body in an angular motion. 

In the case of bodies that are free to move and rotate in a three-dimensional axis, the trends can be defined with the 3 × 3 symmetric matrices. We all are aware that in cases of linear situations, the momentum of a body is conserved (law of conservation of momentum), so this goes similar to angular motions as well. Here, in angular acceleration, the angular momentum of a body defined as the moment of inertia × angular velocity remains fixed in a body. 

The moment of inertia units is asserted as 

1) kg m² (kilogram meter squared), which is the SI unit of Moment of Inertia 

2) lbf ft s² (pound-foot second squared), which is the part of US or imperial units. 

Moment of Inertia Formulas 

1) Scientifically, we define the Moment of Inertia as the product of the mass of a section of the body and the squared result of the distance between the centroid and the reference axis of the body. 

2) The Moment of Inertia is given by the formula as                                

                             I = L/ω

To keep the angular momentum constant in a rotating body, as the size of the moment of inertia goes down, the angular velocity must compulsorily increase to balance and equalize the situation and keep the angular momentum of a body constant. 

3) In the cases, when the shape of the body doesn’t change, the moment of inertia is defined as the ratio of the applied torque on a body with the angular acceleration of a body.

                           I = τ/α

4) In the case of a simple pendulum, the moment of inertia is defined in terms of the mass and distance undertaken from the pivot point or the axis.

                          I = mr²

5) There can be another case too, where the moment of inertia is defined in terms of the mass of the body and the effective radius of gyration of the body undertaken from the particular axis motion which takes place in the body. 

                          I = mk²

Factors which Moment of Inertia depends on 

From the above definitions, we might infer that the Moment of Inertia of a body depends upon the mass of that particular object. However, it is not only the mass on which the Moment of Inertia depends on, but it is also the distribution of this specific mass in a body that affects the body too. 

Moment of Inertia usually relies upon the principle of the axis and the upright distance of the axis of the body to the objects’ mass, for its value. Here, the objects’ mass specifically directs to the center of mass of a body where all the mass of the object is collected at a single point on the plane. However, it should also be noted that moment of Inertia does not depend on the angular velocity of the body for its values. 

Moment of Inertia in various shapes of body

1) Moment of Inertia of a solid sphere is defined in terms of the mass and radius of the uniform spherical object. It is described by the formula 2MR²/5.

2) Moment of Inertia of disc is also defined in terms of the radius and mass of the object. It is given as I = MR²/2.

3) Moment of Inertia of a hoop about diameter is given by the formula same as that of the moment of inertia of disc. It is explained as MR²/2. 

4) In the case of Rod about the center, the formula for moment of inertia is given as ML²/12. 

5) The most different of all is the case of a solid cylinder’s central diameter. The moment of inertia for this shape is given as (MR²/ 4) + (ML²/12). 

Exemplary questions

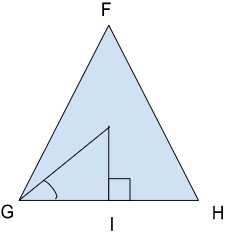
Question: Suppose three wooden stakes are positioned in the pattern of an equilateral triangle. Each of these stakes have length l and mass m. In this context, find the moment of Inertia of the structure that is established by these stakes about an axis passing through its prominent point of the masses and which is upright to the plane. 

Answer: 

Let’s consider FGH as the three sides of the equilateral triangle. Here, the perpendicular intersects the midpoint of line GH, at point I. From the centre of the masses, a line also connects side G, forming a 30° angle. 

So, the moment of inertia for the wooden stick GH can be shown as the formula I_GH = ML²/12. 

Now, the moment of inertia for this wooden stick GH about the asked axis can be explained through parallel axis theorem

                                             I = ML²/12 + ML (1/2√3)

                                                 I₁ = ML²/6

So, the Moment of Inertia of all the three wooden sticks is given as: 

                     I = 3(ML²/6) 

                      I = ML²/2

Conclusion 

Thus, we can define moment of inertia as the multitude which specifies the amount of torque that is needed to put a body in an angular motion. Similar to the case of linear situations, as the momentum of a body is conserved (law of conservation of momentum). Here, in angular acceleration, the angular momentum of a body (defined as moment of inertia × angular velocity) also remains fixed in a body. Notably, the concept of moment of inertia has a major role in the area of rotational kinematics presently and future as well.