Watch Free Classes

What is the spring-mass system?

In the real spring-weight system, spring has a negligible weight m. Since not all spring lengths are as fast v as the standard M, its kinetic power is not equal to (½)mv². Therefore, m will not automatically be added to M to determine the rotation frequency, and the active spring weight is defined as the weight that needs to be added by to M in order to predict system behavior accurately.

Hooke’s Law

The simplest oscillations occur when the restoring force is directly proportional to displacement. The name that was given to this relationship between force and displacement is Hooke’s law:

F = k.x

Here, F is the restoring force, x is the displacement from equilibrium or deformation, and k is a constant related to the difficulty in deforming the system (often called the spring constant or force constant).

Time Period of Spring-Mass 

A common example of back-and-forth opposition in terms of restorative power equals directly shifted from equality (i.e., following Hooke’s Law) is the state of the mass at the end of a fair spring, where “right” means no real-world variables interfere with the perceived effect.

Bulk movement in the spring can be defined as Simple Harmonic Motion (SHM), which is a term given to the oscillatory movement of a system in which total energy can be defined according to Hooke’s law. Now we can decide how to calculate the time and frequency of the weight around the end of the appropriate spring. T-time can only be calculated by knowing the magnitude, m, and constant force, k:

So we can say the time period is equal to

We can understand the dependence of these figures on m and k in an accurate way. If one were to increase the volume in the oscillating spring system by a given k, the increasing magnitude would provide additional inertia, resulting in acceleration due to the ability to return F to decrease (remember Newton’s Second Law:

F = ma

This will extend the oscillation time and reduce the frequency. Conversely, increasing the constant power of k will increase the recovery power in accordance with Hooke’s Law. 

Period of a Mass on a Spring

The period of a mass m on a spring of constant spring k can be calculated as 

For spring, we know that F=−kx, where k is the spring constant.

Let’s discuss spring-mass arrangements.

Spring mass systems can be arranged in two ways. These include;

  • The parallel combination of springs
  • Series combination of springs

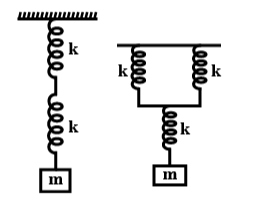
The first picture shows a series, while the second one shows a parallel combination.

What is the time period when in parallel

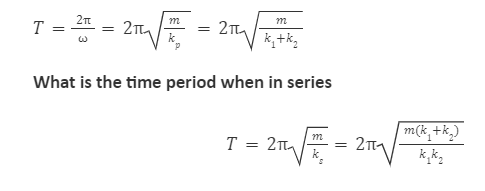
These are very important equations that’ll help you solve problems. 

Points To Remember

  • When an object vibrates to the right and left, it must have a left-handed force when it is right and a right-handed force if left-handed.
  • The regenerative force causes the oscillating object to revert back to its stable equilibrium, where the available energy is zero.
  • The simplest oscillations occur when the recovery force is directly proportional to the displacement. In this case, the force can be calculated as F = -kx, where F is a positive force, k is a positive force, and x is positive.
  • Bulk movement in the spring can be described as Simple Harmonic Motion (SHM): an oscillatory movement that follows Hooke’s Law.
  • The bulk time in the spring is given by the equation

  T=2 π√mk     

Important Goals

  • Restorative energy: Flexible energy creates balance in the body system. If the system is disrupted from equity, the recovery power will be inclined to restore the system to equity.
  • The ability to restore only the function of weight or particles. It is always directed back to the equilibrium area of ​​the system
  • Amplitude: The maximum value of a specific value.

Conclusion

We can conclude by saying that the spring-mass theory is very crucial in the electronics industry. Now we understand and analyze what the working principle is, we now know the equation that can be used to solve theories and problems.