Dimensionless Quantity

A dimensionless quantity is a quantity that has no dimension which means it is a unitless or a scalar number resulting from computations using the same dimensional quantities. In various fields such as mathematics, physics, chemistry and economics, dimensionless quantities are commonly used. Dimensionless quantities are different from quantities that have dimensions, such as length (measured in meters). They are physical quantities that have no specified dimensions and are one (1). Some examples of dimensionless quantities are,

• Strain

• Mass fraction

• Molar fraction

• Relative humidity

• Mach number

• Specific gravity

• plane angle, solid angle 

Check out the complete UPSC Syllabus

DIMENSIONLESS QUANTITIES:

Dimensionless quantities can be divided into two types based on their dimensions.

(i) Dimensionless variables: Dimensionless variables are physical quantities that do not have dimensions but have a changeable value.  They are produced by multiplying and dividing combinations of physical variables, parameters, and constants. Examples are specific gravity, strain, and refractive index.

For example

 Angle

As angle in radians is the ratio of arc to the radius, dimensions of length get cancelled resulting in dimensionless quantity.

(ii) Dimensionless Constant: dimensionless constants are those quantities that have no dimensions and have a constant unchangeable value. Examples are π, e, numbers etc

pi (π)

pi is the circumference to radius ratio. As a result, it lacks dimensionality.

Its value is approximately equal to 3.14159

Also see: UPSC Question Paper

History of Dimensions Quantity

Dimensionless quantities are those Quantities having dimension one, they are common in science and are formally handled in the discipline of dimensional analysis. French mathematician Joseph Fourier and Scottish physicist James Clerk Maxwell pioneered key advancements in the contemporary ideas of dimension and unit in the nineteenth century. Osborne Reynolds and Lord Rayleigh, both British scientists, later contributed to the knowledge of dimensionless quantities in physics. Edgar Buckingham derived the π theorem (independent of French mathematician Joseph Bertrand’s prior work) to codify the nature of these quantities, based on Rayleigh’s approach to dimensional analysis. In the early 1900s, a slew of dimensionless numbers, principally ratios, were invented, especially in the fields of fluid mechanics and heat transfer.

Visit to know more about How to Prepare for UPSC without Coaching

A dimensionless quantity may have a unit

A unit does not always have to be a physical one.  As a consequence, a dimensionless quantity is independent of the base unit at all moments. moles, kilograms,  candela, kelvin, and meter, ampere, second.

Other quantities, on the other hand, are dimensionless yet have a unit. An angle, for example, is measured in radians. However, because it is defined as the ratio of two lengths, it has no dimensions.

 A radian isn’t a fundamental unit of measurement. It’s a derivative unit.

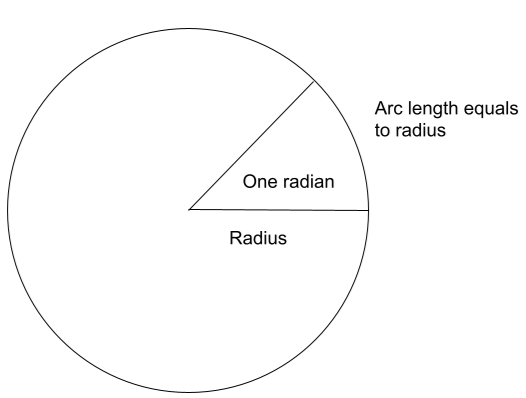
In general, the angle subtended at a circle’s centre, measured in radians, is equal to the ratio of the contained arc’s length to the radius’s length. This ratio is dimensionless since the units of measurement cancel. Since it is the ratio of two lengths, a radian is a derived unit, not a fundamental unit. The radian (a unit of plane angle) and the steradian (a unit of solid angle) were once classified as ‘supplementary units,’ a class distinct from fundamental or derived units. However, because they were the sole supplemental SI units, they were subsequently categorized as derived SI units as well.

Conclusions

Dimensionless quantity units, often known as one-dimensional quantity units, “1”. Certain quantities are dimensionless or have a dimension that can be described by number one since they are defined as the ratio of two similar values. Because the unit must be the ratio of two identical SI units, the number one is the coherent SI unit for all such dimensionless quantities or quantities of dimension one.

The units are not clearly stated, and the values of all such quantities are simply presented as numbers., friction coefficient, relative permeability, and refractive index are only a few examples of such values.