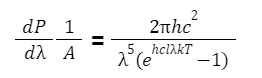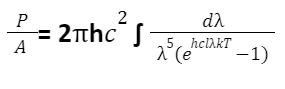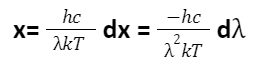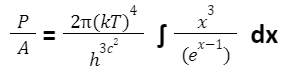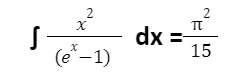Derivation of Stefan Boltzmann Law

Stefan Boltzmann law is also called Stefan’s law. This law is basically based on the concept of black bodies in physics.  

The Stefan Boltzmann Law is especially used for the black bodies to determine the light radiating from them. Joseph Stefan the scientist who gave the Stefan Boltzmann law deduced the conclusions made from the Tyndall effect of light and came up with this law. 

Another law in this concept is Wien’s Law that helps to determine the exact wavelength at which the power peaks at. The Stefan Boltzmann law helps to determine how much the Sun emits given its hot temperature throughout. 

It is because of Stefan’s Law that the scientists have been able to understand the temperature of the sun and its degree of hotness and also the power generated by the Sun because of its high temperature. 

As we all know that the Earth receives the heat from the Sun, so it is possible with the help of Stefan Boltzmann law to deduce the heat that is emitted by the Earth when the heat from the Sun falls on its surface. 

History

In 1864, John Tyndall provided ed measurements of the infrared discharge through a platinum filament and the analogous color of the filament. The proportionality to the fourth power of the supreme temperature was inferred by Josef Stefan (1835–1893) in 1879 based on the Tyndall’s experimental measurements, contained in the article Über die Beziehung Zwischen der Wärmestrahlung und der Temperatur (On the association among thermal radiation and temperature) in the Bulletins from the assemblies of the Vienna Academy of Sciences.

An origin of the law from theoretical contemplations was provided by Ludwig Boltzmann (1844–1906) in 1884, focusing upon the thesis of Adolfo Bartoli. Bartoli, in 1876 had obtained the subsistence of radiation pressure from the standards of thermodynamics. Subsequent to Bartoli, Boltzmann deemed a perfect heat engine utilizing electromagnetic radiation rather than a perfect gas as a working matter.

Stefan-Boltzmann’s law of radiation experiment was nearly verified. Heinrich Weber, in 1888 spotted differences at higher temperatures; however, ideal precision within measurement uncertainties was corroborated up to temperatures of 1535 K by 1897. The law, comprising the theoretical calculation of the Stefan–Boltzmann constant as a role of the speed of light, the Planck’s constant and the Boltzmann constant, is a direct outcome of Planck’s law as devised in 1900.

Derivation of the law

The entire power for each unit area from a black-body radiator could be attained by incorporating the Planck radiation formula above all wavelengths. The exuded power for each unit area as a purpose of wavelength is: 

Consequently, the integrated power implies

It is supportive to build the substitution

Carrying the substitution offers

Making usage of the standard form integral

Provides the concluding form of the Stefan-Boltzmann law

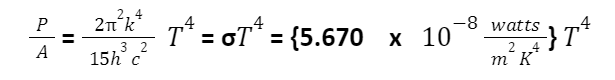
Examples

The temperature of the Sun

Through his law, Stefan as well resolved the temperature of the Sun’s surface. He deduced from the statistics of Jacques-Louis Soret (1827–1890) that the energy flux density through the Sun is 29 times higher than the energy flux density of a particularly warmed metal lamella (a thin plate). 

A round lamella was put at such a distance from the computing gadget that it would emerge at the same angle as the Sun. Sort approximated the temperature of the lamella to be roughly 1900 °C to 2000 °C. 

Stefan deduced that ⅓ of the energy flux through the Sun is soaked up by the Earth’s atmosphere. Thus he took for the right Sun’s energy flux a value 3/2 times higher than Soret’s value, specifically 29 × 3/2 = 43.5.

Specific measurements of atmospheric inclusion were not created until 1888 and 1904. The temperature Stefan attained was a median value of the preceding ones, 1950 °C and the utter thermodynamic one 2200 K. As 2.574 = 43.5, it follows from the law that the temperature of the Sun is 2.57 times higher than the temperature of the lamella; consequently, Stefan attained a value of 5430 °C or 5700 K (the modern value is 5778 K). 

This was the sensible primary value for the temperature complying with the Sun. Previous to this, values scaling from as low as 1800 °C to as high as 13,000,000 °C were asserted. The lower value of 1800 °C was verified by Claude Pouillet (1790–1868) in 1838 utilizing the Dulong–Petit law. Pouillet moreover took only half the value of the Sun’s right energy flux.

Conclusion

The Stefan – Boltzmann Law compacts with the black body radiation. It affirms that the overall energy radiated for each unit surface area through a black body in unit time is directly proportional to the fourth power of thermodynamics temperature of the black body.