The moment of inertia is a crucial concept that appears in almost all physics scenarios that include mass in rotating motion. The Moment of inertia or MOI is most commonly used to determine angular momentum or rotational motions. Let us discuss this moment of inertia or MOI in the coming paragraphs.
Let us understand from a basic what a moment of inertia is defined as:
The moment of inertia commonly referred to as the rotational inertia or angular mass is a number that defines the rate of torque necessary for a specific angular acceleration or speed or quality of an object that opposes the angular acceleration or speed when measured about the axis of rotation. The addition of the masses of the objects” of each object along with the distance’s square from the rotational axis” is the calculation equation for the MOI.
If we speak in simple words a moment of inertia is the amount by which anybody is resisting the angular acceleration forced onto it.
If we speak about the SI unit of MOI or the moment of inertia. It is Kg m^2. Having its dimensional formula is as [M1L2T0].
A rotating axis is widely used to indicate the moment of inertia. It is mostly determined by the mass distribution around a rotational axis. The MOI changes based on which axis is selected.
Let us now look at the formula and other important aspects related to the moment of inertia.
The Formula of Moment of Inertia or MOI
In general, as said in the introduction it is the product of the masses of the objects and the square of the distance of the object from the rotational axis. Which when represented in the form of an equation will be as.
I=M × r²
Where,
I = Moment of inertia
M = Mass of the object
r = object’s distance from the rotational axis
If we represent the above equation in its integral form. It will be as,
I= ∫dl=M × r²
If we talk about the difference between inertia and the MOI. The difference would be that the moment of inertia is related to the rotation of objects. However, inertia is related to the linear motion of objects. Such as the inertia of a bus travelling in a particular direction and the moment of inertia of an I-section beam subjected to a particular load.
The formula of the moment of inertia when having multiple objects
When multiple objects are there then the calculation of the MOI can be done by using the integral form of the equation also there are some other formulas given below, also refer to the diagram for better understanding:
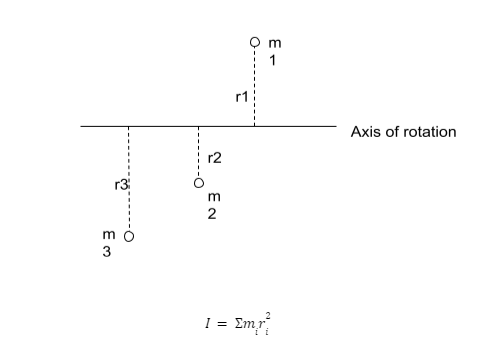
Where,
m = mass of the object
r = distance form the axis of rotation
i = notation of the particular particle or object.
Moment of Inertia factors
Like several other variables, MOI also depends on various values and variables. Which are mentioned below in points:
- The cross-sectional shape and dimension of the substance. For example, if the shape of the cross-section is an I section, it would have a different particular value. If the shape of the cross-section is rectangular it would have a different moment of inertia value. If the shape is triangular It would have a different value. Similarly, every cross-section has a different formula and value. However, all the formulas for every cross-section shape are derived from its base formula which is given above.
- Another factor for the moment of inertia is the density of the object as it would decide the mass which is a crucial component in finding the moment of inertia of any object or particle.
- The third and last factor is the rotational axis and also the number or distribution of objects are there around the axis of rotation.
Conclusion
To sum up, an MOI is also called the angular momentum or acceleration which is done for rotating objects similar to inertia. However, it is quite different from linear inertia as the name itself suggests that inertia is for linear motion and moment of inertia is for angular motion or rotational motion.
The base formula for finding the moment of inertia as well as for deriving the equation or moment of inertia of other cross-sections is the product of mass and the square of the distance of the particular object from the axis of rotation and when there are multiple particles present the formula would be the product of the sum of all the masses and the square of the distance of particles from the axis of rotation.
Also concluding the factors of the MOI as it depends on a few factors, such as the size and shape of the cross-section of the object such as I cross-section, circular cross-section or rectangular cross-section, etc and another factor is the density of the object, and the last and final is the distribution of particles and objects about the rotational axis.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out













