Profile
Settings
Refer your friends
Sign out
The moment of inertia is also referred to as the momentum inertia or the rotational inertia. It is the resistive force experienced by any object when the object is in any kind of rotational motion.
Speaking about the MOI or the moment of inertia of an annular disk. Before going into that we must understand what an annular disk is. An annular disk is similar to a normal disk. However, unlike a normal disk, it has a hollow space inside it. Therefore, it has two radii, an inner radius and an outer radius. To find out the moment of inertia of an annular disk, we will consider a small elemental ring inside the annular disk having a radius of r and width of dr along with the thickness t. That can also be considered as the small elemental volume inside the annular disk. We are initially going to find out the moment of inertia of that ring or the elemental volume and then integrate it having the limitations of the radius of the disk to find out the moment of inertia of the complete annular disk.
To get an idea the moment of inertia of an annular disk is given by the equation,
I=1 ⁄2M(R2²+R1²)
Where,
M denotes the annular disk’s mass
R1 denoted the annular disk’s inner radius
And R2 denotes the annular disk’s outer radius.
In this article, we are going to learn how to derive the moment of inertia formula of an annular disk
Derivation
Before going into the derivation, let us understand the annotations used and the annular disk using a diagram.
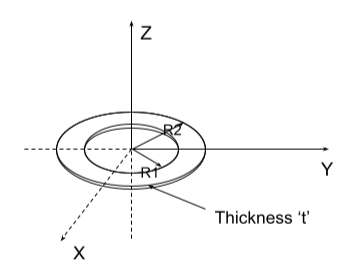
Consider an annular disk having a thickness as ‘t’, inner radius as ‘R1’ and outer radius as ‘R2’. The axis of rotation in this derivation is considered the Z-axis, which is also the axis of the disk itself.
Also consider the small elemental volume inside this annular disk having radius r, thickness t and width dr. This elemental volume can also be considered a ring.
To start the derivation initially we will take the general formula for the moment of inertia of any small elemental object, which is,
dI=r²dm …………….1
So, according to this the moment of inertia of our considered elemental ring would be,
I=0Rr²dm
Now we need to find out the mass of the ring, in respect of volume and density which is given as,
dm=dV
Where,
dV=(2rdr)t
So, from using the equation of volume mass’s equation will be as,
dm=(2t)rdr
Now, we’ve found the mass of the small elemental volume. We’ll integrate this small mass in the moment of inertia formula using the limits of the integration as R1 and R2.
And thus, the equation of moment of inertia of annular disk using equation 1 can be rewritten as,
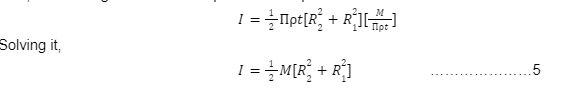
Here we go, equation 5 is the desired equation of the moment of inertia of an annular disk or mass moment of inertia of an annular disk.
Conclusion
To sum up, the moment of inertia of an annular disk can be found by initially taking a small elemental volume, specifically an elemental ring and finding out the mass of that small ring and using that mass in the equation of the moment of inertia of the disk and then integrating the equation having the limits between the two radii. At a step, we again need to find the mass of the disk to solve the equation, thus finding the same by subtracting the mass of the whole disk with radius R2 from that of R1 and substituting the value and solving it. At last, we will find the moment of inertia of a complete annular disk.
