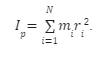Calculating Moment Of Inertia Of A Hollow Cylinder

In this article, we will unfold an interesting chapter in physics: the moment of inertia. Today, we will specifically focus on the moment of inertia of a hollow cylinder. Now, all physics enthusiasts might know that this topic is extremely important but many students get confused while studying it. 

This is because there are a lot of technicalities in the moment of inertia. Although if you understand the core concept and formulas properly then this topic won’t give you any headaches. So, grab a pen and paper and let’s understand how to calculate the moment of inertia of a hollow cylinder without any complications.

Also see:

• IAS Coaching in Mukherjee Nagar Delhi
• IAS Coaching in Karol Bagh
• UPSC Coaching in Prayagraj

What is the Moment of Inertia?

Moment of inertia can be defined using the concept of the rotational axis, as a quantity that helps in measuring the amount of torque (a force that can cause an object to rotate about an axis) required for a desired angular acceleration. It is also commonly known as mass moment of inertia or rotational inertia.

Now, the value of the moment of inertia can vary depending on which position of the axis is chosen. The SI unit of the moment of inertia is kg.m².

Visit to know more about How to Prepare for UPSC without Coaching

Moment of Inertia of a Hollow Cylinder:

Here, we will consider the moment of inertia of a hollow cylinder that is rotating on an axis passing through the centre of the cylinder. For this calculation, we will use an internal radius r1and external radius r2. As we know the moment of inertia is incomplete without the mass M so we will be using it as well. So, the final equation we get is as follows:

I= 1 ⁄ 2 M (r2² + r1²) 

Likewise, we can also get the moment of inertia of a hollow cylinder with a thin wall;

I=Mr²

I know you have a lot of confusion regarding the derivation of these equations. Don’t worry, keep reading the article as down below we will tell you  how to calculate the moment of inertia of a hollow cylinder in great detail.

Also read UPSC syllabus pdf download

Calculation of the Moment of Inertia of a Hollow Cylinder:

Let’s break down the components of a hollow cylinder: inner radius r¹, outer radius r² with mass M and length L. For now, we will calculate the moment of inertia of a hollow cylinder about the central axis. Before, we start calculating keep the following things in mind: The cylinder is split into extremely small thin rings and each ring has a thickness of dr with length L.

Now, let’s start the calculation of the moment of inertia of a hollow cylinder:

First, we will start from the moment of inertia equation;

dl=r²dm

Here, we need to find dm;

dm= dV

Since dV is present in the above equation we need to carry out the further calculation as follows;

dV=dA h

Here, dA is the area of the ring on top;

dA=π (r+dr)² – πr²

dA=π (r²+2rdr+(dr)²)– πr²

Here, (dr)²=0

dA= 2 r dr

Finding the value of dA using the differentiating method;

A=r²

Differentiating w.r.t r;

dA=2 r dr

Substituting dA into dV;

dV=2 r h dr

Substituting into dm;

dm= 2 r h dr

Next, we substitute the dm expression into the dl equation;

dl=r² 2 r hdr

dl= 2 r³ h dr

Now, it’s time to find the expression for density, for this we use the following equation;

= M/V

=M / hπ(r2² – r1²)

To finally get the moment of inertia we need to integrate the inner radius to the outer radius;