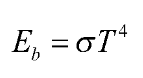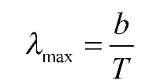An ideal blackbody absorbs all incident energy and reflects or transmits none. It is a model that may be used to compare the radiation properties of real bodies. Any incident radiation, regardless of wavelength or direction, is absorbed by a blackbody. A blackbody’s energy output is a function of its temperature and is not evenly distributed across all wavelengths.
The radiation inside an enclosure with its inner walls kept at a constant temperature has the same qualities as blackbody radiation and is referred to as such. A blackbody radiator is also known as an ideal radiator.
Blackbody Radiation
When a body is heated above absolute zero, it emits radiation in all directions and at a wide variety of wavelengths. The amount of radiation energy radiated by a surface at a given wavelength is determined by the body’s composition, the condition of its surface, and the temperature of the surface. As a result, various bodies may produce varying amounts of radiation per unit of surface area.
Despite the fact that they are at the same temperature. As a result, it’s only natural to wonder what the maximum amount of radiation a surface may produce at a particular temperature is. This curiosity necessitates the creation of an idealised body known as a blackbody that can be used to compare the radioactive features of real surfaces.
Joseph Stefan computed the radiation energy released by a blackbody per unit time and per unit surface area in 1879 and stated it as
Where, is
The Stefan-Boltzmann constant and the absolute temperature of the surface is in K.
is known as the blackbody emissive power.
Stefan-Boltzmann law
The Stefan-Boltzmann law states that the total radiant heat output emitted from a surface is proportional to its absolute temperature to the fourth power.
Here,
E is the radiant heat energy radiated from a unit area in one second
T is the absolute temperature (in kelvins)
The Greek letter sigma indicates the Stefan-Boltzmann constant. The value of this constant is
Only blackbodies, theoretical surfaces that absorb all incident heat radiation, are subject to the law.
Planck’s law
Max Planck derived the relation for the spectral blackbody emissive power in connection with his famous quantum theory in 1901, called Planck’s law. Planck made an assumption that radiation originates from oscillating atoms and that the energy to cause a vibration of each oscillator can never be in between but in a series of different values and can be expressed as,
Here, is the absolute temperature of the surface,
is the wavelength of the radiation that is emitted, and Boltzmann’s constant is
. This relation is only true when the surface is in a vacuum or a gas. It must be modified for other mediums by substituting
with
, where n is the medium’s index of refraction. The term spectral denotes a wavelength-dependent relationship.
Wein’s Displacement law
The overall radiated energy increases as the temperature of a blackbody radiator rise, and the peak of the radiation curve shifts to shorter wavelengths. This relationship is known as Wien’s displacement law used to calculate the temperatures of hot radiant objects like stars, as well as any radiant object whose temperature is much higher than its surroundings.
Wein’s displacement law for the spectral blackbody is mathematically expressed as,
where,
Blackbody radiation Graph and observations
This figure shows a plot of Wien’s displacement law, which is the locus of the radiation emission curves’ peaks, from which the following observations were made:
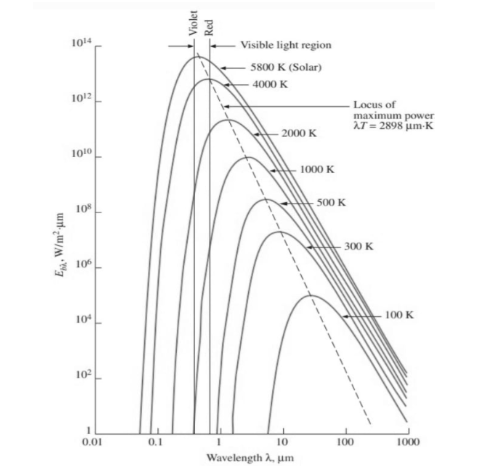 • As the temperature rises, the curves shift to the left, toward the shorter wavelength region. As a result, at higher temperatures, a greater proportion of the radiation is emitted at shorter wavelengths.
• As the temperature rises, the curves shift to the left, toward the shorter wavelength region. As a result, at higher temperatures, a greater proportion of the radiation is emitted at shorter wavelengths.
• The peak of the curve in the given figure shifts toward shorter wavelengths as temperature rises. Wien’s displacement law gives the wavelength at which the peak occurs for a given temperature as
Example 1
A black body emits radiation at 2000K. Calculate (a) monochromatic emissive power at wavelength (b) maximum emission wavelength and (c) the maximum emissive power.
Solution:
Given:
To find:
(a) By Planck’s law,
…..(1)
(b) By Weins law,
Now, substitute value of equation (2) in equation (1)
(c) According to Stefan Boltzmann Law,
⸫The maximum emissive power is
Applications of blackbody radiation
• The black bodies are used in applications such as lighting, heating, security, thermal imaging, and testing and measuring.
• Planck’s Law of Radiation can be used to determine the intensity of energy at any temperature and wavelength. For calibrating and testing radiation thermometers, a blackbody radiation source with a known temperature or whose temperature can be measured is commonly utilised.
• The Boltzmann distribution will be the spectrum of light coming out of the hole if the piece of metal is heated to a uniform temperature. Black bodies are useful for calibrating thermal cameras and other detectors by establishing consistent Boltzmann spectral distributions.
Conclusion
All incident radiation is absorbed by an ideal blackbody, and none is reflected or transmitted. It’s a model that can be used to compare real-world radiation properties. The energy output of a blackbody is a function of its temperature and is not spread uniformly across all wavelengths. Theoretically, black bodies are surfaces that absorb all incident heat radiation. Mathematically, it is described by Stefan-Boltzmann law, Planck’s law, and Wein’s displacement law.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out