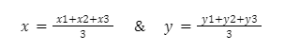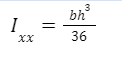Profile
Settings
Refer your friends
Sign out
Moment of inertia of a triangle can be demonstrated in many ways. There are, in general, three moments that can be considered and an axis passing through its centroid is one of them. The three ways are:-
- An axis passing through its centroid
- An axis passing through its base
- An axis perpendicular to its base
What Is A Centroid?
The centroid (also known as center of gravity) of any shape or an object is the center point within that object from which the force of gravity appears to act. An object will remain stationary if it is balanced on any point along a vertical line that is passing through its centroid.
The center of gravity of a 2 dimensional surface is a point that corresponds to the center of gravity of a very thin homogeneous plate of the same area, figure,section and shape. If the area (or figure or section or body) has a single line of symmetry, the centroid will lie somewhere along the line of symmetry.
Deriving The Expression
Moment of inertia of a triangle about an axis passing through its centroid can be worked out using the application of parallel axis theorem:
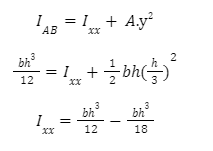
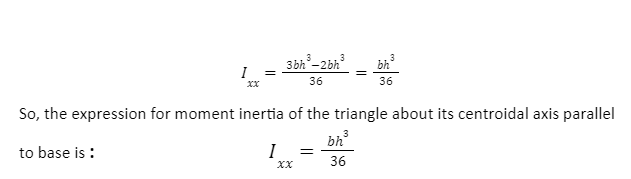
Centroid Of A Triangle
We will understand the centroid of a triangle with the help of an example:
Suppose there is a beautiful garden near my house which is triangular in shape. We decided to build a fountain in the center of the garden but as we already know that the garden is triangular in shape, how can we find the center of the garden? Here mathematics comes into the picture to help us and in math the center of an object or a shape is called the centroid of that object or shape. The word “Centroid” is used as a substitute for a term such as center of gravity or center of mass. It is a point that balances the shape but since we are talking about the triangular garden, The centroid of the triangle is the balancing point created by the intersection of three medians whereas median is the line drawn from the midpoint of one side of the triangle to the opposite vertex. Now to find the centroid of the garden, the first thing we need is to draw the medians. For the ease of understanding let us name the garden as ABC. First we will find the midpoint of side BC naming it as D and join the midpoint D to the opposite vertex i.e. vertex A. Here, we got median AD. Similarly draw median BE and median CF. Now we can see that the three medians are intersecting at a common point and this intersection point is our centroid denoted by point G.
Properties Of Centroid Of A Triangle
- It divides all the medians in the ratio of 2 : 1 which means that if we go from the vertices to the centroid then the length is 2/3 of the entire median and if we move from the centroid to the base then the length is 1/3 of the entire median.
- It divides the area of a triangle in three equal parts
- Median divides the line in two equal parts
- Median divides the area of a triangle in two equal parts
- Any two sides of a triangle are together greater than twice the median drawn on the third side.
Deriving the Centroid Formula
To derive the centroid formula :-
- Find the midpoint of any one side using the midpoint formula
- Then apply the section formula to obtain the centroid formula
Let’s understand it with the help of the example we took above:-
How to find the median of this garden? We will take the help of coordinate geometry. Let’s suppose A, B, and C are the coordinates of the vertex of the garden. Which more points will require the coordinates now? So, these are point D, E, and F. Let’s find the first coordinates of point D. It is the midpoint of side BC.
Conclusion
After getting familiar with the above mentioned topics, we can conclude that the centroid of a triangle is the intersection point derived as the three median of that triangle meets. We came through the theoretical as well as practical aspect of the centroidal axis with the help of an example that makes it easy to learn in a hassle free manner.
