Profile
Settings
Refer your friends
Sign out
Moment of inertia of different shapes can be demonstrated in many ways. There are, in general, three ways that can be considered in general and an axis passing through its base is one of them. Those three ways are:-
- An axis passing through its centroid
- An axis passing through its base
- An axis perpendicular to its base
What Is The Moment Of Inertia?
According to Newton’s first law of motion, every body continues in its state of rest or of uniform linear motion, unless an external force acts on it to change that state. This inability of the body to change by itself, its state of rest or of linear uniform motion is called inertia. Similarly, a body rotating about a given axis tends to maintain its state of uniform rotation, unless an external torque is applied on it to change that state. This property of a rigid body as a result of which it opposes the torque tending to bring changes in its stationery state or of uniform rotation about its axis is referred to as moment of inertia.
Definition:- The moment of inertia of a rigid body about a fixed axis is defined as a sum of the products of the masses of the particles constituting the body and the squares of their corresponding distances from their axis of rotation.
Moment Of Inertia Of An Axis
Moment of inertia of an axis can be defined as the product of these two: –
- mass of section
- square of distance between the reference axis and the centroid of that section
Moment of inertia of an axis can also be defined as the ratio of these two around a principal axis:-
- Net angular momentum of the system:- It is the vector sum of the individual angular momentum of the system about its axis.
Its angular velocity:- It defines the speed with which a body rotates with regard to its center of rotation.
It can be expressed as I=l ⁄ w
Where, I = Moment of Inertia
l = angular momentum, and
W = angular velocity
Thus the moment of inertia of a body about an axis is numerically equal to the angular momentum of the rigid body when rotating with unit angular velocity about that axis.
Moment Of Inertia Of A Rectangle Passing Through its Base
The moment of inertia of a rectangle about an axis passing through its base can be numerically expressed as follows:-
I=bh³ ⁄ 3
Where, b = base width of the rectangle, and h = height of the rectangle
It is worked out by applying the Parallel Axis Theorem because the centroid of a rectangle is located at a distance equal to h ⁄ 2 from the base.
Formula For Moment of Inertia Of A Hollow Circular Cone
- Hollow cone:- A hollow cone is a geometrical shape that resembles a pyramid but with a difference that it is hollow from inside.
- Mass of a hollow cone
- Radius of a hollow cone: Half of the diameter of the hollow cone
The moment of inertia of a hollow circular cone can be numerically expressed as:
I=MR² ⁄ 2
Where, I = Moment of Inertia
M = mass of the hollow cone, and
R = radius of the hollow cone
Moment Of Inertia Of A Triangle
Moment of inertia of a triangle about an axis passing through its base can be worked out as follows:-
Consider a triangle ABC. Base = b & Height = b.
Consider an elementary strip PQ at a distance x from vertex A.
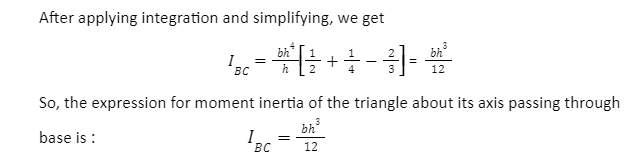
Conclusion
This article has summed up the moment of inertia of a few common shapes that is generally found everywhere on earth. This holds its application in the practical world a lot and thus is an important topic to consider. We have learnt the meaning and formulas of the moment of inertias of a rectangle, a hollow circular cone.
