Understanding Permutation And Combination

Permutations and combinations are widely used to solve the questions of probability. In probability, they are used in various types of questions, and that’s why permutations and combinations form the distinctive principle of counting. However, both permutations and combinations are similar, but the order of sets separates them. Permutations are used in the ordered sets, while combinations are used in the unordered sets. Permutations can be described as the arrangement of sets, while combinations can be described as the selections of sets. Although,  there are the separate sum and product rules of permutations and combinations for making the computation easy. 

Permutations 

The arrangement of data in the definite sequence is called permutations. The process of performing permutations is called permuting. So, permuting is arranging the set in a specified order and set. It can also be defined as rearranging the sets of elements of sets in an ordered set, called permutations. Permutations can only perform in the ordered sets. 

Combinations 

The selecting or grouping of data is called combination. In combination, the order of the sets does not matter. It can apply to unordered sets. In simple words, the combination is taking out the k element from the set. Repetition is not allowed in combinations. 

Permutation formula 

Let’s learn about the permutation formula. 

The permutation is arranging r elements from the n set of multiple elements in a definite manner. Replacement is not allowed in the permutation, and it can be performed only on ordered sets. 

Permutation formula: 

nPr =  (n!)/(n-r)!

Here, [n > = r]

 r = Selected element 

 n = number of all elements. 

In the set of multiple elements, the elements must be ordered. 

Combination formula 

Let’s learn about the combination formula

Combinations are replacing, grouping or selecting elements from their set. The selection of r elements from n sets. The formula of combination is written as, 

nCr = nPr = (n!)/r! (n-r)!

Combination selects elements randomly from the set so that it can be performed on unordered sets. 

Other formulas of permutations and combinations 

Let’s learn about the different formulas of permutations and combinations. 

To count or observe a set suitable for permutations or combinations. Some formula that comes under permutations and combinations:

Formula 1: 

Factorial formula 

The factorial is the product of all natural numbers, which are less than the given n. The formula of factorial. 

n! = 1 × 2 × 3 × 4 × …….× n

Formula 2: 

Permutation case: where the reputation of elements is allowed. 

The permutation value of n set, where r element is taken. 

Formula: nr 

Formula 3: 

Permutation value of n set, where the elements are taken in a group at a time. In this set, p1 is the first element, p2 is the second element, and k is the kth element. 

The formula is as follows: 

Permutation = (n!) / p1. p2…. Pk

Formula 4: 

The formula describes the relationship between permutations and combinations. 

nPr = r! × nCr

Applications of permutations and combinations

Let’s learn about the different applications of permutations and combinations.

Permutation 

• A permutation is used to arrange the groups or sets. For instance, arranging of numbers, peoples, digits and letters. 

• It is also used to pick or select one thing from the group or set. For instance, picking or selecting one captain from the team. 

• Picking fruits from the basket, picking the best colour from the colours, etc. 

• Picking the players for first, second and third position. In this, all the team members are arranged in the ordered sequence, according to their capabilities. 

Combination 

• The combination is used to select one thing from various varieties. For instance, selecting clothes from the cupboard, selecting food from the menu, etc. 

• It is also used to pick or select an option from the group or sets, irrespective of its order and quality. 

• It is used to select two colours for mixing from various shades. 

• Selection of good players from the team. 

Permutations and combinations questions 

Let’s understand some permutations and combinations of questions

Q: Find the value of permutations and combinations, if n = 4 and r = 2

Answer: 

Permutation:

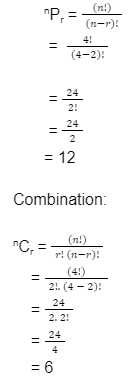
So, the value of permutations and combinations is 12 and 6.

Conclusion 

Permutations and combinations both are the selection process, but the only difference lies in their orders. A permutation is picking the best elements from the arranging elements, for instance, if the students are standing in a sequence of their rank. Then a selection of the first three best students for the quiz is the permutation. The combination is the random pick of the element from the group. In the above example, the selection of any three students for the quiz, irrespective of their rank, is a combination. Although, the selection of elements is common in permutations and combinations.