Truth Tables For Unary Operations

A truth table is used for logical specification in context with boolean algebra, boolean functions and propositional calculus. It sets the functional values of logical expressions by using boolean operators of their functional arguments. It has a column for each input variable and a resultant column showing all possible results of the logical operations. It has four unary operations Logical True, Logical false, Logical identity, and Logical negation. Unary Operations are such operations that take only one input, the NULL operator and the NOT operator. The NULL operator will represent the same result as of input, but in the case of the NOT operator, it will represent the opposite result.

Truth table

A Truth table is a table in which Boolean Operators are used for evaluating expressions. In the truth table, one column is used for each input, and another column represents all the possible results of the logical operations. The truth table is a table that breaks down logic functions by listing all possible values. A truth table may contain several rows and columns. The top row represents the logical variables and combinations. The truth table logic gates give us all the information about the combination of inputs and outputs for the logic operation. In a truth table, a statement is called a contradiction if the final column of that truth table contains only 0’s. If the final column of that truth table contains both 0’s and 1’s, this is called contingency or contingent. A truth table shows the truth values of a statement formula for every combination. A statement with only one of the two possible values is called truth values. A truth table for Unary operations is an operation that deals with only one operand.

Where Binary operations are such operations that deal with two operands but here we are just discussing unary operators, i.e. with a single or one operand. Before starting unary operations, we must be clear with boolean operators. So let’s know about boolean operators.

Boolean operators were invented by a mathematician named George Boole. He invented Boolean algebra, the mathematical system which underlies logic in computers. Boolean algebra is a branch in mathematics that deals with different operations on logical values. Three basic boolean operations are AND, OR, NOT. 

AND:- Its basic work is to satisfy both the conditions. 

OR:- Its basic work is to satisfy anyone’s condition as if either first or second any of the conditions are true, it will work.

NOT:- It reverses the value. If the operand is false, it returns true, and if it’s true, it returns false.

There are four unary operations:-

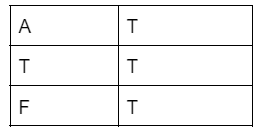
1. Logical true 

In the true logical case, whatsoever the input is, the output is always true whatever the input is. The truth table for logical true is:- 

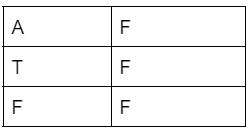
2. Logical false

In the false logical case, the output is always false, whatever the input is. The truth table for logical false is- 

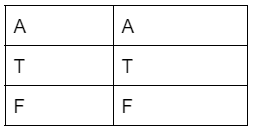
3. Logical identity  

In the logical identity case, the output remains the same as the input. The truth table for logical identity is:- 

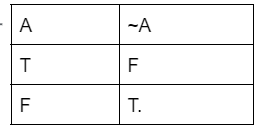
4. Logical negation  

In the logical negation case, the output comes opposite of the input (means in case the input is true, the output comes false, and in case the input is false, the output comes true.) The truth table for logical negation is- 

After discussing the above unary operations, now the turn for NOT and NULL Operators.

NULL Operator:- If the input of value A  is 0, the NULL will produce output 0, and if the input of A is 1, the NULL will produce 1.

NOT Operator:- If the input of value A  is 0, the NOT will produce output 1, and if the input of A is 1, the NULL will produce 0.

Table for Unary Operations:-