Trigonometric ratios relate the ratio of sides of a right triangle to the respective angle in trigonometry. The basic trigonometric ratios used in trigonometry are sin, cos, and tan, namely, sine, cosine, and tangent. Other important trigonometric ratios are cosec, sec, and cot, derived from sin, cos, and tan. The word “Trigonometry” was derived from the words “Trigonon”, which stands for “Triangle”, and “metron”, which means ” to measure”. In the Trigonometric table, we use the values of Trigonometric ratios for some standard angles that are 0°, 30°, 45°, 60°, and 90°.

What are Trigonometric ratios?

Trigonometric ratios include six ratios, namely sine, cosine, tangent, cosecant, secant, and cotangent. In short, these ratios are written as sin, cos, tan, cosec, sec, and cot. Trigonometric ratios relate the ratio of sides of a right triangle to the respective angle in trigonometry. These ratios are used for any two sides of a right-angled triangle with any respective angle.

Trigonometric ratios formulas 

Trigonometric ratios are also calculated by taking any two sides of a right-angled triangle. After finding two sides, we can easily find the third side of the triangle by using the Pythagoras theorem. In trigonometric ratios, the angle at the base is compared with Any two sides of a triangle. The angle being compared is generally known as angle θ, an acute angle,0°<90°. The basic Trigonometric formulas of Trigonometry are as follows:-

• tan θ = Perpendicular/Base

• sec θ = Hypotenuse/Base

• cosec θ = Hypotenuse/Perpendicular

• cot θ = Hypotenuse/Perpendicular

• sin θ = PerpendicularHypotenuse

• cos θ = Base/Hypotenuse

Now let us take a look at the reciprocal of the given Trigonometric formulas, as we know that sin θ is the reciprocal of cosec θ, tan θ is a reciprocal of cot θ, and cos θ is a reciprocal of sec θ therefore, the common set of Trigonometric formulas is:-

• tan θ = 1 / Cot

• cosec θ = 1 / Sin

• sec θ = 1 / Cos

• cot θ = 1 / Tan

• sin θ = 1 / Cosec

• cos θ = 1 / Sec

Trigonometric table 

In the Trigonometric table, we use the values of Trigonometric ratios for some standard angles that are 0°, 30°, 45°, 60°, and 90°. The values of the Trigonometric table are easy to predict, and the table is used as a reference for the Trigonometric ratios during calculation for various other angles. Now we are summarising the Trigonometric ratios for the specific angle of specific Trigonometric formula in the Trigonometric table given below:-

Trigonometric ratios identities

We use many trigonometric identities to make our calculations simpler and easier. These identities include supplementary angles, complementary angles, Pythagoras identities, and product, sum, and difference identities.

-Trigonometric ratios of complementary identities

The pair of angles whose sum of angles equals 90° are known as complementary angles. The complement for any angle θ is 90°- θ, therefore Trigonometric ratios used for complementary angles are:-

• sec (90°- θ) = cosec θ

• tan (90°- θ) = cot θ

• cot (90°- θ) = tan θ

• sin (90°- θ) = cos θ

• cos (90°- θ) = sin θ

• cosec (90°- θ) = sec θ

-Trigonometric ratios of Pythagoras’s identities

Pythagorean Trigonometric identities are derived from Pythagoras’ theorem.

• sin2θ + cos2θ = 1

This is the important Pythagoras identities from which we can derive 2 more identities-

• 1 + tan2θ = sec2θ

• sin2θ + cos2θ = 1

• 1 + cot2θ = cosec2θ

-Trigonometric ratios of sum, difference and product

Trigonometric ratios of sum, difference and product include formulas such as sin(A+B), sin(A-B), cos(A+B), cos(A-B), etc.

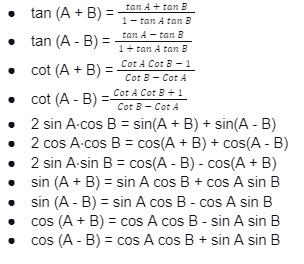
Conclusion:

Trigonometric ratios include six ratios, namely sine, cosine, tangent, cosecant, secant, and cotangent. Trigonometric ratios are also calculated by taking any two sides of a right-angled triangle. After finding two sides, we can easily find the third side of the triangle by using the Pythagorean theorem. The values of the Trigonometric table are easy to predict, and the table is used as a reference for the Trigonometric ratios during calculation for various other angles. Trigonometric ratios include six ratios, namely sine, cosine, tangent, cosecant, secant, and cotangent. In short, these ratios are written as sin, cos, tan, cosec, sec, and cot.