Profile
Settings
Refer your friends
Sign out
The inverse of a Matrix
The inverse matrix is the other matrix that, when multiplied with the given matrix, would give its multiplicative identity. For a square matrix A, the inverse would be A-¹, and AA-¹ = A-¹A = I, which is known as the identity matrix.
A matrix with a non-zero determinant as well as the one whose inverse could be calculated is known as an invertible matrix.
The formula of an Inverse Matrix:
The inverse of a real number x is x-¹, and x.x-¹ = 1. This is similar to the inverse matrix system, where a square matrix A and its inverse A-1, when multiplied, result in an identity matrix I.
Formula:
A-¹ = 1 ⁄ A
. Adj A, where Adj is the adjoint of the square matrix A.
Adjoint matrix: The transpose of the matrix of the cofactor of elements of A is known as the adjoint of matrix A.
Here, as A lies at the position of the denominator, thereby it has to be non-zero for the inverse matrix formula to exist. So, A ≠0.
Properties of an Inverse Matrix:
- Every invertible matrix possesses a unique inverse.
- A square matrix is invertible if it is non-singular.
- Law of Cancellation: Let A, B, and C be square matrices of the same order n. If A is a non-singular matrix, then
AB = AC B = C
BA = CA B = C
4. Law of Reversal: If A and B are invertible matrices of the same order n, then AB is invertible and (AB)-1 = B-1A-1.
5.If A is an invertible square matrix, then AT is also invertible and (AT)-1 = (A-1)T.
6.The inverse of an invertible symmetric matrix is a symmetric matrix.
7.Let A be a non-singular square matrix of order n. Then, adj A = An-1.
8.If A and B are non-singular square matrices of the same order, then adj AB = (adjAB)(adjA).
9.If A is an invertible square matrix, then adj AT = (adj A)T.
10. If A is a non-singular matrix, then
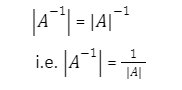
Elementary Operations of a Matrix:
A matrix obtained from an identity matrix by a single elementary operation (transformation) is called an elementary matrix.
There are three operations to be applied to the rows/columns of a matrix:
- Interchange of any two rows/columns
- Multiplying all elements of a row/column of a matrix by a non-zero scalar.
- Adding to the elements of a row/column, the corresponding elements of any other row/column are multiplied by any scalar k.
Finding the Inverse of a Matrix by Elementary Transformations:
Let A be a non-singular square matrix of order n. Then A can be reduced to the identity matrix In by a finite sequence of elementary transformations only. As every elementary row transformation of a matrix is equal to pre-multiplication by the corresponding elementary matrix, therefore there exist elementary matrices
Inverse Matrices for solving Linear Equations
For a 22 square matrix, it can be calculated with the help of a simple formula. However, for determining the inverse of a 33 matrix, we would need to find the adjoint and the determinant of the matrix as well. The inverse matrix method can be used to determine the solutions of linear equations. It is also helpful in determining the consistency or inconsistency of the solutions to linear equation problems.
This method is applicable only if:
- The matrix is a square matrix
- It has to be non-singular
Let us consider a matrix equation.
AX = B, (i)
where A is a non-singular square matrix.
As A is non-singular, A-¹ would exist and A.A-¹ = A-¹A = I.
Multiplying (i) both sides by A-1, we get
A(A-¹)X = (A-¹)B
Therefore, X = A-¹B
It is important to be noted down that the multiplicative order as followed above needs to be kept in mind as it is not arbitrary.
Conclusion:
In this article, we saw an overview of the inverse matrix. The inverse matrix is the other matrix that, when multiplied with the given matrix, would give its multiplicative identity. For a square matrix A, the inverse would be A-¹, and AA-¹ = A-¹A = I, which is known as the identity matrix. We also saw the formula used along with the properties of an inverse matrix. Inverse matrices are helpful in determining the solutions of linear equations and also checking the consistency or inconsistency of these solutions.
