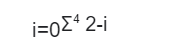SERIES IN MATH

Understanding series and sequences is extremely useful and applicable in various fields such as computer programming, designing, finance, statistics and physics. A sequence, also called a progression, is defined as the arrangement of individual terms in an orderly manner. These individual terms of a sequence, when added together, give rise to a series. Therefore, a series is the sum of terms in a progression. The order of elements or terms is important in a sequence but not in a series. These series and sequences can be classified into arithmetic progression, geometric progression, harmonic progression and Fibonacci progression.

SERIES AND SEQUENCES:

Series and sequences can be classified as finite or infinite. A finite sequence is where the last term of the sequence is known. For the following progression,

2,4,8,16,32,64, the series is calculated as follows:

2 + 4 + 8 + 16 + 32 + 64

also denoted as,

i=1Σ6 2i

This is the summation of the sequence with index ‘i’ having a lower limit of 1 and an upper limit of 6 for the general sequence 2 raised to the power of the index.

Types of series and sequences:

 ARITHMETIC PROGRESSION AND SERIES:

A series in which each element or term is derived by addition or subtraction of a fixed number from the preceding term is called an arithmetic series and be represented as,

a + a+1d + a+2d + a+3d +….+ a+ nd

where a: first term in the sequence

         d: common difference

         n: the number of terms

The nth term in an A.P. is given as,

an = a+ (n−1)d 

The series for a finite arithmetic progression is given as,

Sn = n/2 (2a + (n−1)d)

where Sn: Sum of first n terms in the sequence

GEOMETRIC PROGRESSION AND SERIES:

The summation of a list of numbers in a sequence where each term is derived by multiplication or division of a constant ratio from the preceding term is called a geometric series, and the sequence is called a geometric progression or G.P. A geometric series can be represented as,

a + ar + ar2 + ar3 + … arn – 1

where r: common ratio

The nth term in a geometric progression is given as,

nth term = a rn-1

The series for a geometric progression is given by the formula,

Sn = a (1 – rn) / (1 – r)

where Sn: Sum of first n terms.

Let’s take an example. Calculate the sum of the first 9 terms for the given G.P. 3, 6, 12, 24, 48… and so on.

The sum of first 9 terms can be given as,

n=0Σ9 3(2)n

= Sn = a (1 – rn) / (1 – r)

S9 = 3(1 – 29) / (1 – 2)

= 1533 

HARMONIC PROGRESSION:

The sum of a list of terms present in a sequence such that each element or term is derived from the reciprocal of the corresponding term in an arithmetic progression is called a harmonic series, and the sequence is called a harmonic sequence or H.P. In other words, it is the series of reciprocals of terms in an A.P. It can be represented as,

1/a1 + 1/a2 + 1/a3 + 1/a4 + … +1/an                

Where a1, a2, a3, a4, … an is the arithmetic progression.

The nth term and series of the harmonic progression can be calculated by the formulas,

1/an = 1/ [a+(n-1)d]

Sn= 1/d (ln(2a + (2n – 1)d) / (2a – d))

Where ln is the natural logarithm.

An example of the harmonic series is as follows:

1/2 + 1/4 + 1/6 + 1/8 + 1/10 + …. +1/2n.

 Or, i=1Σ∞1/2i

FIBONACCI SEQUENCE:

A Fibonacci series is the addition of terms in a sequence in which each term is the sum of two preceding terms, starting with 0 and 1 as the first two terms. Therefore, it can be represented as,

0 + 1 + 1 + 2 + 3 + 5 + 8 + 13… and so on.

Here, F0 = 0, F1 = 1, F2 = 1, Fn being the nth term in the Fibonacci series.

The nth term in the Fibonacci series is given as,

Fn = Fn-1 + Fn-2       

where Fn-1 and Fn-2 are the terms preceding the nth term