A non-monotonic function is the one whose first changes signs mean the increasing to the decreasing. Thus, it is increasing or decreases for some time or after some interval and it shows different types of behavior at different locations. The quadratic function y = x 2 is a classic example of a simple non-monotonic function. The functions which perform both increasing as well as decreasing in their specific domain are known as non-monotonic function.
What Is Monotonicity?
The monotonicity of a function helps us in determining whether the function is increasing or decreasing in nature. A function is increasing when it shows in the graph an upward direction from point a to point b. If for any x1 and x2 in I, x1 is a smaller amount than x2 implies that f(x1) is a smaller amount than f(x2). This says that when x1 is a smaller amount than x2, then the function evaluated at x1 is a smaller amount than the function evaluated at x2.
What Is Monotonic Function?
A Monotonic Function is stated as any given Function that follows one of the four cases mentioned above. The Monotonic term is derived from the two terms first one is Mono refers to at least one and tonic refers to tone from these two-term we get monotonic. After you say that a Function is non-Decreasing, does it mean that it’s increasing? The solution is not any. It may also mean that the Function doesn’t vary in the least. In simpler words, the Function has a continuing value for a specific interval. Confirm to not confuse non-Decreasing with Increasing.
What Is Non-Monotonic Function?
A non-monotonic function is a function that shows increasing or decreasing behavior for some time or after some interval and it shows different types of behavior at a different position It is those functions whose first derivative changes signs frequently.. y = x2 is the best example of a non-monotonic function. The functions which are increasing as well as decrease after some intervals are known as non-monotonic functions.
Non Monotonic Graph
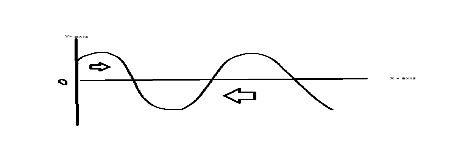
A non-monotonic function is a function that is increasing and decreasing at different intervals of its domain as you can see in the above figure.
For example, as you can see in the above figure that in the graph there is no proper increasing or decreasing function they get an increase or decrease in certain intervals in their certain domain is known as the non-monotonic function. As you can see both the increasing as well decreasing trends in the graph so these type of trends is known as the non-monotonic function.
Non-Monotonic Increasing Function
As we know that increasing function means that an upward line going through the graph or if the second point within the graph is larger than the primary point within the graph then it’s called the increasing function but in the case of non-monotonic function the upward line is increases or decreases in some of the interval time or a particular period so this process is known as the non-monotonic increasing function. This experiment is clearly shown in the above figure. In the non-monotonic increasing function, the graph shows both the aspects increase as well as decrease so this process is known as the non-monotonic increasing function
Non-Monotonic Decreasing Function
It can describe as after we are ready to see a downward line going through the graph or if the second point within the graph is smaller than the primary point within the graph then it’s called decreasing function. But in the case of the non-monotonic decreasing function, the downward line is increases or decreases in some of the particular time frame so this process is known as the non-monotonic decreasing function. . In the non-monotonic decreasing function the graph shows both the aspects increases as well as decreases so showing this process is known as a non-monotonic decreasing function
Conclusion
The monotonicity of a function helps us in determining whether the function is increasing or decreasing in nature. A function is increasing when it shows in the graph an upward direction from point a to point b. If for any x1 and x2 in I, x1 is a smaller amount than x2 implies that f(x1) is a smaller amount than f(x2). This says that when x1 is a smaller amount than x2, then the function evaluated at x1 is a smaller amount than the function evaluated at x2. A non-monotonic function is a function that shows increasing or decreasing behavior for some time or after some interval or in a particular time frame and it shows a different type of behavior at a different position in the graph. It is that function whose first derivative changes signs frequently.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out











