Monotonicity in an Interval

Monotonicity refers to a function that has the attribute of either never rising or never decreasing when the values of the terms’ independent variables rise. The word monotonic can also refer to set functions that translate domain subsets to non-decreasing codomain values. In mathematics, what monotonicity tells us is if the function is increasing or decreasing.

Monotonicity of a Function

A monotonic function is one that is either fully non-increasing or completely non-decreasing. The monotonicity of a function indicates whether it is rising or decreasing.

If the graph of a function climbs from left to right, it is rising. If the graph of a function falls from left to right, it is diminishing.

The monotonicity of a function is proportional to its derivative.

Monotonicity on its domain

The growing or decreasing tendency of a function on its domain is referred to as monotonicity.

Increasing Function

A function is said to be having increasing monotonicity at an interval when the value of the function increases as the independent value.

That is, if x1>x2, then f(x1) > f(x2).

Therefore, when x2 is less than x1, then the function evaluated at x2 is less than the function evaluated at x1.

Decreasing Function

A function is said to be having decreasing monotonicity at an interval when the function value decreases as the independent value increases.

This indicates that if x1 is greater than x2, then f(x1) f (x2).

Therefore, when x2 is less than x1, then the function value of x2 is greater than the function value of x1.

A function’s monotonicity and derivative

The monotonicity of a function is proportional to its derivative.

When the derivative of a function is positive, the function increases, and when the derivative is negative, the function decreases.

For example, considering the function f(x)= x²

f’ (x) = 2x is the derivative. Consider when 2x is both positive and negative.

The value of 2x is larger than zero.

Dividing both sides by 2

x yields a result larger than zero.

As a result, f’ is positive when x is bigger than zero. As a result, if f increases on the interval x is bigger than 0,

Consider the case when 2x is negative, that is, if 2x is less than 0.

Dividing both sides by 2

x yields a result smaller than 0.

Thus, f’ is negative when x is less than zero, and f decreases when x is less than zero.

Test for Monotonicity

Finding the growing and decreasing range for the function f(x) = x²- 4 explains the monotonicity test.

The function f(x) = x² – 4 is a polynomial function that is continuous and differentiable in its domain (-, +), satisfying the criteria of the monatomic function test. The function’s derivative must be determined in order to determine its monotonicity. That is

df(x)/dx = d(x² – 4)/dx

              = (d(x²) – d(4))/dx

              = 2x

It is evident that the function df(x)/dx = 2x is negative when x is zero and positive when x is greater than zero. As a result, the function f(x) = x² – 4 increases in the range (-, 0) and decreases in the range (0, +).

Finding monotonicity at an interval of a function

Knowing the monotonicity of a function, now we can find the intervals of the function which are rising or falling.  We analyze its first derivative f’(x).

If the function is increasing at a point, the derivative is positive; otherwise, it is negative.

The derivative’s root is a point where the function is neither rising nor decreasing.

We can still determine its monotonicity in the intervals between the roots if it contains one or more roots. To determine the monotonicity of a function in an interval when it is rising or falling, we must first discover the roots of the derivative. The function can shift from falling to rising at certain places and vice versa. If the derivative is positive on the left and negative on the right of this point, we know it is transitioning from rising to sinking. As a result, we may examine the derivative values immediately left and right of the root.

Conclusion

Finding the growing and decreasing intervals of the function, say y = (x-1)², can help you understand the notion of monotonicity. The function decreases in the interval [-, 1]. The function is rising in the interval [1, +]. The function, however, is not monotonic in its domain (-, +).

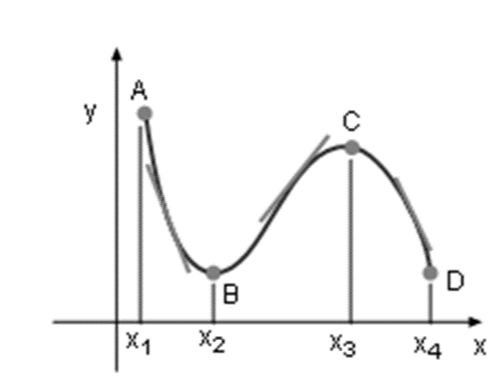
The function is decreasing in [x1, x2] and [x3, x4] in the Derivative and Monotonic in the graph below, and the slope of the function’s tangent lines is negative. The function, on the other hand, is rising in [x2, x3], and the slope of the function’s tangent line is positive.