Profile
Settings
Refer your friends
Sign out
Before we move on to the different formulas concerning straight lines it is important to understand the meaning of straight lines. A line that is infinite in length without any twists and turns is known as a straight line. The formation of a straight line takes place when the two points A (x1, y1), and B (x2, y2) are connected with the minimal distance between them. These lines are extended to infinity.
The above figure gives a clear understanding of a straight line. A line in which there is no beginning nor any end.
Types of Straight Lines
The segmentation of the straight lines can be done into 3 types, which include the following:
- Horizontal line
- Vertical line
- A slanted or oblique line
Horizontal line
The line that is perpendicular to the axis of ‘y’ or parallel to the axis of ‘x’ is termed a horizontal line. They form an angle of 180 degrees or zero degrees with the x-axis and an angle of 90 degrees or 270 degrees with the y-axis.
Vertical line
The line that is perpendicular to the axis of ‘x’ and parallel to the axis of ‘y’ is known as a vertical line. The line, with the x-axis form an angle of 90 degree or 270 degrees and an angle of zero degrees or two hundred and seventy degrees with the y-axis.
Slanted line
A slanted line is also known as an oblique line. A slanted line is drawn in a position that is slanting in shape. It can also be stated as a line that forms an angle other than zero degrees, ninety degrees, one hundred and eighty degrees, two hundred and seventy degrees and three hundred and sixty degrees.
Equation of a straight line
The equation of a straight line is linear. Based on the constants, variables and angles, a straight line on a Cartesian plane have various presentations. The direction of a straight can be understood by the slope of the straight line and can also be found out how steep the straight line is.
General Equation of the straight line.
The representation of the general equation of a straight line can be done in the following way, ax + by + c = 0.
In the above equation, it is to be understood that,
The alphabets a, b and c are constants. The alphabets x and y are variables. The slope is -a/b.
Formulas for the pair of straight lines
The formula for the pair of straight lines can be written as,
(a{x2} + 2hxy + b{y2} = 0) this represents a second-degree homogenous equation. It shows two straight lines that are passing from their origin. Thus,
- ({h2} > ab) The equation is relatable when both the straight lines are different and real.
- ({h2} = ab) The equation is relatable when both the straight lines coincident.
- ({h2} < ab) The equation is relatable when the straight lines have an origin as the intersection point and are imaginary.
Equation of the straight lines that are parallel to the x or the y axis.
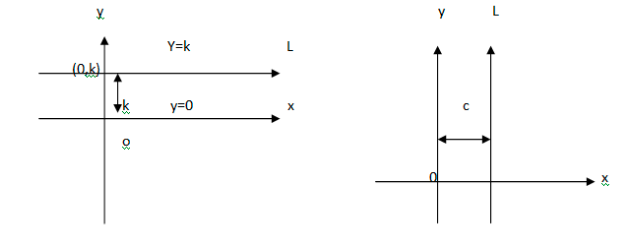
The equation of the straight line that is parallel to the x-axis is denoted by, y = ±a, the following condition is satisfied when from the x-axis a happens to be the distance of the straight line from the x-axis. The value of ‘a’ remains positive if the value remains above the axis of x. The value becomes negative if the value remains below the axis of x. Â
In the same way, the equation of the straight line that is parallel to the y axis is denoted by x = ±b, the following condition is satisfied when b happens to be the distance of the straight line from the y-axis. The value of ‘b’ remains positive if the value remains above the axis of y. The value becomes negative if the value remains below the axis of y. Â
Conclusion
A straight line is a joining of numerous points in a single direction without the formation of any type of twist and turns. There are three forms of the straight lines and one thing that needs to be noted here is that all of these lines are formed without any hurdles or are neither with any form of twists and turns. Various equations are been framed to find the outcome of the straight lines in different forms.
