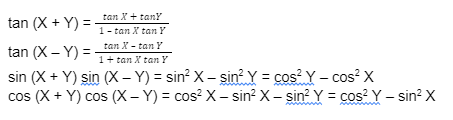Profile
Settings
Refer your friends
Sign out
Compound angles can be demonstrated as the integration of angles. These angles are defined as the sum of two angles of a triangle. These angles are widely used in trigonometry. In compound angles, the two angles of the triangles are added. After their addition, a unique identity forms. And if this unique identity forms using the trigonometric functions, they are called the trigonometric identities. The concept of trigonometry is mostly based on the right-angle triangle. The trigonometry also contains trigonometric ratios like sine, cosine, cosecant, and so forth, which are derived using the Pythagoras theorem of right-angled triangles.
Compound angles
are defined as an addition of two angles. Compound Angles are mainly used in the study of triangles. The study of triangles is also known as trigonometry. So, compound angles also deal with trigonometric ratios. In simple words, compound angles are defined as a sum of two angles and two algebraic quantities, which demonstrate the value of angles.
Trigonometry ratios
are called the standard angles under trigonometry. These ratios are calculated by dividing the different sides of the right-angle triangle. Trigonometry ratios are used to define a particular angle regarding other sides. In trigonometric ratios, all sides related the specific angle mentioned properly. There are six trigonometric ratios.
Cosine or cos y =Hypotenuse / Perpendicular
Sine or sin y = Perpendicular / Hypotenuse
Secant or sec y = Hypotenuse / Base
Cosecant or Cosec y = Base / Hypotenuse
Cotangent or cot y = Base / Perpendicular
Tangent or tan y = Perpendicular / Hypotenuse
Compound angles for trigonometry ratios.
Let’s understand some compound angles of trigonometric ratios.
sin(X + Y) = sinX.cosY + cosX.sinY
sin (X – Y) = sin X cos Y – cos X sin Y
cos (X + Y) = cos X cos Y – sin X cos Y
cos (X – Y) = cos X cos Y + sin X cos Y
tan (X + Y) = tan X + tanY / 1 – tan X tan Y
tan (X – Y) = tan X – tan Y / 1 + tan X tan Y
sin (X + Y) sin (X – Y) = sin2 X – sin2 Y = cos2 Y – cos2 X
cos (X + Y) cos (X – Y) = cos2 X – sin2 X – sin2 Y = cos2 Y – sin2 X
Addition and subtraction of trigonometric ratios with the help of compound angles
Let’s understand the addition and subtraction of different trigonometric ratios. However, four trigonometric equations demonstrate the addition and subtraction based on compound angles. These are:
2 sin X cos Y = sin (X+Y) + sin (X-Y)
2 cos X cos Y = cos (X+Y) + cos (X-Y)
2 cos X sin Y = sin (X+Y) – sin (X-Y)
2 sin X sin Y = cos (X-Y) – cos (X+Y)
Trigonometric ratios table
Let’s learn about the trigonometric ratios table in detail. We also learn about the sin cos table.
The trigonometric ratios table defines the different trigonometric ratios in terms of numeric values. The sin cos table defines the value of sine and cosine at different angles. The trigonometric ratios table is described in two ways. These are
Sexagesimal System
Circular System
Sexagesimal System of trigonometric ratios.
Let’s understand how to describe trigonometric ratios in the Sexagesimal System. In this system, the angle of triangles is described in the form of degrees.
Circular System of trigonometric ratios
Let’s understand how to describe trigonometric ratios in the Circular System. In this system, the angle of triangles is described in the form of radians.
Conclusion
Compound angles are widely used while integrating trigonometric functions. Compound angles are the sum of two angles. Finding the Compound Angles of two trigonometric functions is a simple procedure. Trigonometric ratios are defined as the value of any side concerning its acute angles. Trigonometric ratios define the value of the angles under the different conditions; for instance, cosine demonstrates the angle value while considering perpendicular and hypotenuse. On the other hand, the cosecant demonstrates the angle value while considering base and hypotenuse. All these six trigonometric ratios cover all the conditions for any acute angle.
