Profile
Settings
Refer your friends
Sign out
The median of a triangle is the line segment that joins a particular vertex and subdivides the opposite side of the triangle. To be precise there are exactly three medians that join a triangle from each of the vertices involved to the opposite sides and the lines meet at the centroid. The length of median formula proof determines the value associated with the extent of a particular median. In the case of equilateral and isosceles triangles, the median bisects the angle at the vertices whose adjacent sides are equal to each other.
Length of median formula proof: derivation
The length of the median formula proof determines the value associated span of the medians joining each vertex to the opposite sides of the triangle. The length of the median associated with the various sides of the triangle with sides a, b and c can be derived using a formula
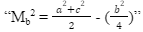
Mb is associated with the median-joining side b of the triangle.
The Length of the formula proof can be derived through the following steps
- In a triangle ABC the sides are to be considered a,b and c. Median Mb is drawn from vertex B
- In consideration of the triangle ABC values are taken from the law of cosines and
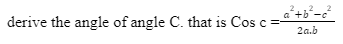
- Furthermore, the triangle is divided into MBC, since the median is bisecting vertex B to side ca at point B, using the laws of cosine the points the square of the median is derived from :
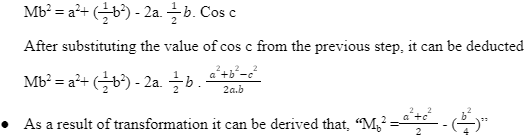
Length of median of equilateral triangle formula
The length of the median is associated with the line that joins a vertex to the equal and opposite sides of the vertices. The median in equilateral triangles intersecting through the centroid and joining the opposite sides are all equal in length. In an equilateral triangle, medians, the bisectors of the angles and the altitude coincide with each other and the ortho-centre, incentre, centroid and circumference also join at the same point. The angles drawn are divided into two equal parts of 30 degrees each. The Length of the median of the
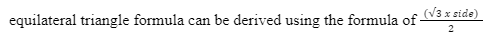
Length of a median of isosceles triangle
In an isosceles triangle, the sides are all equal to each other and they meet each other at the same point. The medians joining each side of the triangle divide the triangle into six smaller triangles. The length of medians of the isosceles triangle joining the vertices to the opposite sides of the triangle have an equal subdivision of the angle due to the passage of medians and the sides are also equally divided since isosceles triangles have two equal sides opposite to each other. The triangle congruence is an attribute of the isosceles triangle that can be used to determine a particular property of it. The method of triangle congruence can be used to derive that in an isosceles triangle the median-joining from the vertex of one side to the base of the triangle is always perpendicular to the base.
Conclusion
In the case of different triangles, the median is the span of a line that joins the vertex of one side of the triangle to the side of the opposite of the triangle. In the case of isosceles and equilateral the median joins the opposite sides at an equal length. The length of the median can be derived using the length of median formula proof that provides the numerical value associated with the particular median-joining each side of the triangle that coincides through the centroid.
In an equilateral triangle, the medians are all equal in length to each other. In an isosceles triangle, the angle which is equal in length when bisected gives a median of equal length. Another property of isosceles triangles is that using the value of triangular congruence it can be derived that the median drawn to the base of the triangle is perpendicular to the base.
