The formula that is to be used for deriving appropriate results of “quadratic vertex” is “x=-b2a”. In order to find the range of quadratic equations or “standard function of quadratic equations”, a specific formula is needed to be followed that is “f(x) =ax2+bx+c”. In this case, a parabola vertex is necessary to find the range of quadratic equations. It is also important to check whether the “vertex of the parabola” is opening upwards or downwards in the quadratic equation. The structure of the quadratic function mainly denotes the range and domain of the given mathematical equations.
Derivation of range and domain using the algebraic form
In order to derive the range and domain of the quadratic equations or quadratic functions algebraically, three main forms of “quadratic equations” are to be considered. In order to achieve the goal of determining the correct way of opening the quadratic functions and to find the coordinate “y” of the vertex, the standard formula is provided as “f(x) =ax2+bx+c”. To find the range of quadratic equations, for the standard form “f(x) =ax2+bx+c”, “a” is positive where the function opens up, but if “a” becomes negative the function will open down. Here, the “y” coordinate of the vertex is calculated by evaluating “f (-b2a)”.
Find the range of quadratic equations
To find the range of quadratic equations or standard quadratic functions a similar process is considered to be used to derive the domain of the quadratic equations. In such a case a horizontal graph is used, where the domain position moves from the left position to its right position along the axis of “x”. The domain of the quadratic equations is determined as all “real numbers”. Apart from using the same approach used in the derivation of the domain, to find the range of quadratic equations it is important to consider the vertical look of the graph. Here the outputs are provided for “y” values which are normally greater than “0”. In some quadratic equations, the value of “y” is also seen as equal to “0” and no outputs are derived in the case of the “x” axis. The range of all “real numbers” remains equal to or greater than “0”.
Finding the range of quadratic by a quadratic equation
For finding the range of quadratic by a quadratic equation, an example has been provided, where the function range of “y” is equal to f(x) is determined as the set of the “y” values for all values of “x” present in the domain “f”. By using quadratic graph and form “f(x) = a x2 + b x + c”, the vertex form can be provided as “f(x) = a(x – h) 2 + k, where h = -b2aand k = f (h)”. This denotes that the vertex parabola either opens up when “a” is greater than 0 or opens down when “a” is less than 0. Hence, if “a” is greater than 0, then the graph “f” will have a minimum point but if “a” is less than 0, the graph “f” will have a maximum point.
How to find a range of variables from the quadratic equation?
In order to find the range of variables from the quadratic equations and from the concept of finding the range of quadratic by a quadratic equation, it can be stated that if the vertex parabola opens up then “a” value will be greater than 0, and if the vertex parabola opens down, the “a” value will be less than 0. It can be further elaborated, that if the “a” value is more than 0, then the “f” graph will have a minimum point, and if the “a” value is lesser than 0, the “f” graph will have a maximum point. Both minimum and maximum values are considered as vertices of
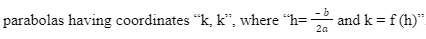
Conclusion
To find the range of the quadratic equations it is important to determine the vertex parabola of the given equation and after that only it can be determined whether the parabola opens down or up. The quadratic form vertex can be obtained by applying the formula, “x=−b2a”. The range of the quadratic functions can be determined as the set of all “possible outputs”. Domain in quadratic functions is considered as a set of all “possible inputs”. For finding the range of quadratic by a quadratic equation, the formula that is mainly used is “f(x) =ax2+bx+c”.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out













