Geometric Interpretation Of Dot Product

The geometrical interpretation of vectors is essential for the detailed understanding of why we consider projections while solving the problems and the impact it can lay to imagine quickly and come up with a better and quick solution-oriented method while solving vectors-related problems. Since vectors are the quantities that define both magnitude and the direction the object is heading. And vectors can exist not only in a single plane or two-dimensional plane of the paper, but they can also be represented in a three-dimensional plane which is why a vector has components associated with it in all three different directions. These directions are the primary reason for the need to get a gold hold of the geometrical interpretation of vectors. By the end, you will be well grasped by the concepts of the geometrical interpretation of dot product and cross product.

What Is A Dot Product?

The theoretical definition of dot product can be expressed as the multiplication of the respective vectors’ magnitudes and the cosine angle made by the two vectors in between them. The primary purpose of using dot product in multiplying any two vectors is to calculate the magnitude of the resultant vector. In Physics, a dot product is also called a scalar product between two vector quantities. 

The dot product is one of the ways to multiply two distinct or equal vectors.

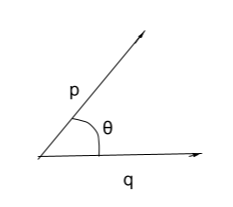
Suppose there are two vectors, namely, vector p and vector q, which are non-zero vectors. Then, the dot product is denoted between p and q is p . q. Here, |p| indicates the magnitude of the absolute value of vector p, and |q| denotes the magnitude of the absolute value of vector q. θ is the angle generated between a and b vectors in the anti-clockwise direction. 

p . q = |p||q|*cosθ

What Is Cross Product?

The cross product is the other common name used to represent a vector multiplication. When two distinct or identical vectors have performed a multiplication, the result will also be a vector of different magnitude and net direction. 

A cross product is done if we consider more about the direction part of the two vectors rather than the magnitudes of the two vectors. When we do the vector product of two vectors with different directions and magnitudes, it is evident that the direction of the resultant vector is found in the third dimension that is mutually perpendicular to the plane of the raw vectors.

Cross Product Formula for three vectors a,b, and c.

To get more clarification, if there are two vectors a and b, and vector a is lying in the X-Y plane, vector b is lying in the Y-Z plane, then when we will do the cross product of vectors a and b, the direction of the resultant vector will lie in the X-Z plane.

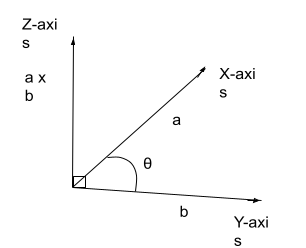
a x b = |a||b|*sinθ

What Is The Geometrical Interpretation Of Dot Product And Cross Product?

The geometrical interpretation of dot product and cross product revolves around the basic skills to use trigonometric functions such as sin, cosine, and tangent in the best possible manner. The projections play a significant role in determining the contribution that one vector puts on the other vector and vice versa.

The geometrical interpretation of the vector product and the scalar product is quite similar and helps us to solve vector problems much quicker than usual. The geometrical interpretation of cross-product requires a good application of determinants and matrix multiplications within a square matrix. 

Geometrical Interpretation Of Dot Product Of Two Vectors 

Suppose there are two vectors, P and Q.

P = a1i + a2j + a3k , and Q = b1i + b2j + b3k

Then, P.Q will define the scalar product.

P.Q = (a1i + a2j + a3k).(b1i + b2j + b3k)

P.Q = {(a1b1)*(i.i) + (a1b2)*(i.j) + (a1b3)*(i.k)} + {(a2b1)*(j.i) + (a2b2)*(j.j) + (a2b3)*(j.k)} + {(a3b1)*(k.i) + (a3b2)*(k.j) + (a3b3)*(k.k)} 

P.Q = a1b1 + a2b2 + a3b3

So, If we place vector a on vector b from the point of their intersection, then the length of vector b occupied by vector a is the projection of a vector a on vector b. It is like the shadow of vector a falling onto vector b. 

• The projection of a vector a on the vector b is calculated by, 

(a.b)/|b|

• The projection of a vector b on the vector a is calculated by,

(a.b)/|a|

• The angle between any two vectors formed by their intersection at one point is calculated by 

Cosθ = (a.b)/|a|*|b|

Geometrical Interpretation Of Cross Product Of Two Vectors

Suppose there are two vectors, P and Q.

P = a1i + a2j + a3k , and Q = b1i + b2j + b3k

Then, P x Q will define the vector product. 

P x Q = (a1i + a2j + a3k) x (b1i + b2j + b3k)

P x Q = (a2b3 – b2a3)i – (a1b3 – b1a3)j + (a1b2 – b1a2)k

If we place vector a on vector b from the point of their intersection, then the length of vector b occupied by vector a is the projection of vector a on vector b. It is like the shadow of vector a falling onto vector b. 

Conclusion

The geometrical interpretation of dot product and cross product revolves around the basic skills to use trigonometric functions such as sin, cosine, and tangent in the best possible manner. The projections play a significant role in determining the contribution that one vector puts on the other vector and vice versa. You learned the geometrical interpretation of dot product and cross product, and the overall geometrical interpretation of vectors.