Derivative Of Dot Product

The dot product is a mathematical operation that takes two vectors as input and produces a scalar value as output. The result is determined by the length of both vectors as well as the angles between them. The total of the products of the matching values of the 2 sequences of numbers is the dot product. It is the product of the Euclidean orders of magnitude of the two vectors as well as the cosine of the angle between them from a geometrical standpoint. In this article, we will look at the derivative of the dot product.

Dot Product

The dot product, also known as the scalar product, is a mathematical operation that yields a single integer from two equivalent sequences of numbers (typically coordinate vectors). The dot product of Cartesian coordinates of two vectors is commonly used in Euclidean geometry. Although it isn’t only one inner product that may be formed in Euclidean space, it is frequently referred to as “the” inner product.

The total of the products of the matching values of the 2 sequences of numbers is the dot product. It is the product of the Euclidean orders of magnitude of the two vectors as well as the cosine of the angle between them from the geometrical standpoint. When utilising Cartesian coordinates, these definitions are equal. In current geometry, vector spaces are frequently used to describe Euclidean spaces. The dot product is used to define lengths and angles in this case 

Derivative Of Dot Product

Vectors are represented in bold little characters, for example, the vector is written by a. The vector a’s length is written in the form a.

Derivative Of The Dot Product Steps

The derivation is carried out in the following ways, starting with trivial evident facts and ending with the concept of the dot product:

• Rectangle’s area

• Right-angled triangle’s area

• The Pythagorean theorem

• Law of cosines

• General triangle’s area using the law of cosines

A Rectangle’s Area

The computation of a rectangle’s area is so simple that a rigorous derivation is unnecessary. The area is just the amount of square units within the rectangle given the breadth a & height b, therefore the area rectangle  = a b.

A right-angled Triangle’s Area 

A right-angled triangle is one in which one of the angles is 90 degrees  The hypotenuse is the side opposing the right angle, while the legs are the other two sides. The area is computed as follows: area triangle = 1/2 a b, where a and b are the two legs.

This is directly taken from a rectangle’s area:

It’s obvious that a rectangle with width a and height b is made of two equal right-angled triangles having legs a & b. So, if two equal triangles form a rectangle having area = a * b, one triangle has 1/2 a b area.

The Pythagorean Theorem 

establishes a relationship between a right-angled triangle’s 3 sides. It claims that the cumulative sum of the legs a & b is equivalent to the square of the hypotenuse c:

c2= a2 + b2

General Triangle’s Area Using Law Of Cosines

The distance equation among two points, which is based completely on the Pythagorean theorem, can be used to construct the law of cosines.

The law of cosines connects the cosine with one angle to the three sides of any triangle. In other words, if you know the lengths of two sides of a triangle as well as the angle between them, you can figure out the length of the third side.

The dot product Derived From The Law Of Cosines.

Finally, we arrive at the dot product, which will be determined using the rule of cosines.

As a result, the length of the triangular side equals the length of vector a, and 

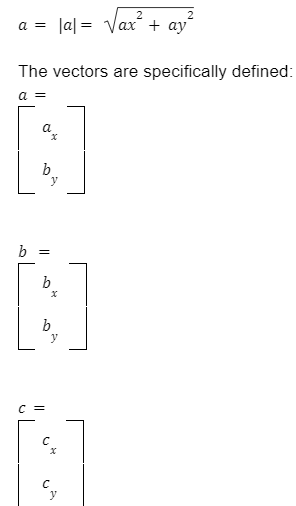
Alternatively, the vector a could be expressed as c – b. Reorganize the solution step by step, changing a and dissolving it, using the law of cosines:

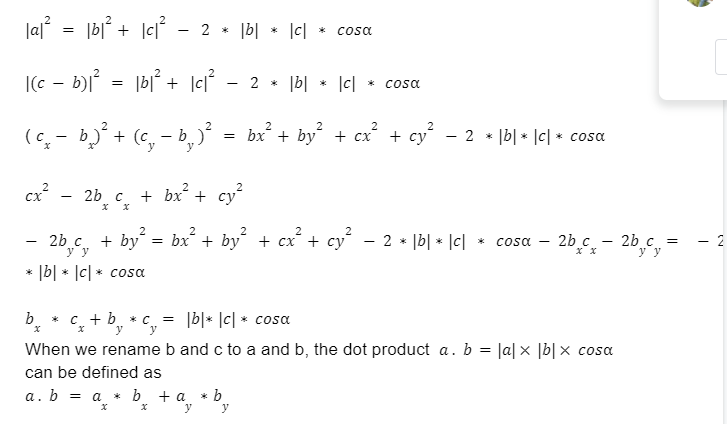
Conclusion

The dot product is a mathematical operation which takes two vectors as input and produces a scalar value as output. The result is determined by the length of both vectors as well as the angles between them. The derivative of the dot product is carried out in the following steps, as discussed in the article: Rectangle’s area, Right-angled triangle’s area, The Pythagorean theorem, Law of cosines and General triangle’s area using the law of cosines.