Corollaries Of Mean Value Theorem

We should now check out three culminations of the Mean Worth Hypothesis. These outcomes have significant results, which we use in forthcoming areas.

The mean worth hypothesis in its advanced structure was expressed and demonstrated by Augustin Louis Cauchy in 1823.

Now, we know the subsidiary of any steady capacity is zero. The generalised mean value theorem permits us to reason that the opposite is additionally evident. Specifically, if f(x)=0 for all x in some span, f(x) is consistent over that stretch. This outcome might appear to be instinctively self-evident. Yet, it has significant ramifications that are not self-evident, and we talk about them without further geometrical interpretation of Lagrange’s mean value theorem.

Corollary 1: Function With A Deviation Of Zero

Allow f to be differentiable over a stretch I. In the event that for(x)=0 for all x∈I, f(x)= consistent for all x∈I.

Verification

Since f is differentiable over I, f should be constant over I. Assume f(x) isn’t consistent for all x in I. Then there exists a,b∈I, where a≠b and f(a)≠f(b). Pick the documentation so that a

f(b)−f(a)b−a≠0.

Since fs has a differentiable capacity, by the Mean Worth Hypothesis, there exists c∈(a,b) with the end goal that

ft(c)=f(b)−f(a)b−a.

Accordingly, there exists c ∈ I to such an extent that if(c)≠0, which goes against the suspicion that if(x)=0 for all x∈I.

Corollary 2: Constant Difference Theorem

On the off chance that f and g are differentiable over a stretch, I and F(x)=g'(x) for all x∈I, then, at that point, f(x)=g(x)+C for some steady C.

Confirmation

Let h(x)=f(x)−g(x). Then, at that point, h'(x)=f'(x)−g'(x)=0 for all x∈I. By Conclusion 1, there is a steady C with the end goal that h(x)=C for all x∈I. Subsequently, f(x)=g(x)+C for all x∈I.

Review that a capacity f is expanding over me if f(x1) <f(x2) at whatever point x1<x2, while f is diminishing over me if f(x)1>f(x2) at whatever point x1

This reality is significant because it intends that for a given capacity f if there exists a capacity F to such an extent that F'(x)=f(x, the different main capacities that have a subsidiary equivalent to f are F(x)+C for some steady C. We examine this outcome in more detail later in the section.

An enigmatically sinusoidal capacity f(x) is diagrammed. It increments from someplace in the second quadrant to (a, f(a)). In this part, it is noticed that if > 0. Then, at that point, it diminishes from (a, f(a)) to (b, f(b)). In this part, it is noticed that if < 0. At long last, it increments to one side of (b, f(b)), and it is noted in this part that if > 0.

On the off chance that a capacity has a positive subsidiary over some span I, the capacity increments over that stretch I; on the off chance that the subordinate is negative over some stretch I, the capacity diminishes over that span I is the generalised mean value theorem.

Corollary 3: Increasing and Decreasing Functions

Allow f to be consistent over the shut span [a,b] and differentiable over the open stretch (a,b).

In the event that f'(x)>0 for all x∈(a,b), f is a rising capacity over [a,b].

On the off chance that f'(x)<0 for all x∈(a,b), f is a diminishing capacity over [a,b].

Verification

We will demonstrate I.; the verification of ii. is comparable. Assume f is certainly not a rising capacity for me. Then, at that point, there exists an and b in I to such an extent that a<b, however f(a)≥f(b). Since f is a differentiable capacity over I, by the Mean Worth Hypothesis, there exists c∈(a,b) to such an extent that

ft(c)=f(b)−f(a)b−a.

Since f(a)≥f(b), we know that f(b)−f(a)≤0. Additionally, a0. That’s what we presume

f'(c)=f(b)−f(a)b−a≤0.

Conclusion

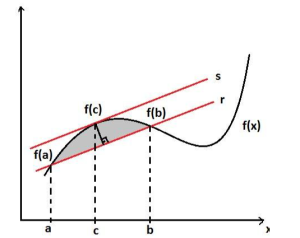
That’s what the mean worth hypothesis expresses, assuming you have a capacity that is ceaseless in a span [a,b], and differentiable in that stretch, then, at that point, there exists some point c where F(c) is equivalent to the slant of the secant line among an and b showing on generalised mean value theorem graph.

Generalised mean value theorem, the three speculations are: f(x) is persistent on [a, b], f(x) is differentiable on (a, b), and f(a) = f(b). the speculation: in our hypothesis, that f (c) = 0. end of a proof. For Rolle’s Hypothesis, concerning most very much expressed hypotheses, every one of the theories is important to determine the end.