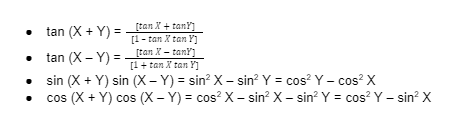Compound Angles

Compound angles come under both geometrical mathematics and trigonometric mathematics. Along with this, it is widely used to know the value of any two angles by integrating them. In compound angles, two angles of the same triangles are summed up. Although angles depict those values, one gets by rotating a ray from its initial point. There are two types of angles: positive angles and negative angles. However, compound angles can be both negative and positive, but only the thing is that they fulfil the requirements of compound angles in mathematics. It comes under both algebra and Trigonometry. 

Compound angles: 

Compound angles are demonstrated as a sum of two angles. It is found under trigonometry. However, when one does not deal with trigonometry, he deals with the algebra compound angles. However, compound angles are the algebraic sum of two angles. 

Trigonometry is limited to right-angle triangles, but compound angles are also found in scalene triangles, isosceles triangles, etc. So, it’s not worth saying that the concept of compound angles is applied only in trigonometry; rather, it applies to the concept of geometry. So any shape whose two-angle sum is equal to 90° has compound angles. 

Calculation of compound angles:

Let’s understand how to calculate the compound angles in detail.

Finding the Compound Angles is the systematic algebraic sum process. It consists of some significant steps. These are:

Step 1

In the first step, one has to find the length of all sides of both triangles. In triangles, the Compound Angles remain between the three sides. So, finding the three sides is very important. 

Step 2 

Take the one-one of both the triangles and calculate the sine angle and cosine angle of both. The formula for finding both the angles is:

• Cosine or cos y = Adjacent Side/Hypotenuse

• Sine or sin y =Opposite Side/Hypotenuse

Step 3

After finding the value of sine and cosine, find the Compound Angles of both the triangles. After that, put the values of sine and cosine values of both the angles in the formula for finding a compound angle. The formula for finding the Compound Angles:

sin(X + Y) = sinX.cosY + cosX.sinY 

So, this is the whole procedure of finding the Compound Angles in trigonometry. However, it can be used to find the angles in other ratios. Trigonometry consists of six trigonometric ratios. These are cosine, sine, cosecant, secant, cotangent, and tangent. Let’s understand the Compound Angles formula for different trigonometric ratios in the next section. 

Compound angles formula for different trigonometric ratios:

There are compound angles formulas for all types of trigonometry ratios. These are:

• sin(X + Y) = sinX.cosY + cosX.sinY

• sin (X – Y) = sin X cos Y – cos X sin Y

• cos (X + Y) = cos X cos Y – sin X cos Y

• cos (X – Y) = cos X cos Y + sin X cos Y

• tan (X + Y) = [tan X + tanY] / [1 – tan X tan Y]

• tan (X – Y) = [tan X – tanY] / [1 + tan X tan Y]

• sin (X + Y) sin (X – Y) = sin2 X – sin2 Y = cos2 Y – cos2 X

• cos (X + Y) cos (X – Y) = cos2 X – sin2 X – sin2 Y = cos2 Y – sin2 X

Sum or subtraction of trigonometric ratios using compound angles:

Let’s understand the sum and subtraction of different cosine and sine angles, which the compound angle formula includes. These are:

• 2 sin X cos Y = sin (X+Y) + sin (X-Y)

•  2 cos X cos Y = cos (X+Y) + cos (X-Y)

•  2 cos X sin Y = sin (X+Y) – sin (X-Y)

• 2 sin X sin Y = cos (X-Y) – cos (X+Y)

Compound angles in other types of triangles: 

Compound angles are mainly used in trigonometry. But, the scope of trigonometry is limited to the right angle triangle. So, if one relies only on the trigonometric compound angles formulas, then what about the other triangles like the scalene triangle and so forth. There are four types of triangles, these are:

• Equilateral triangle 

• Isosceles triangle 

• Scalene triangle 

• Right angle triangle 

However, equilateral triangles are those which have all sides equal. So, in such a triangle, the value of all the angles remains 60° in other triangles, which have a sum of two angles equal to 90°. Then, they consist of compound angles. It can be found within the triangle to check whether it has a compound or not and can be checked between two different triangles by comparing.

Conclusion

Compound angles are widely used in both trigonometry and geometry. They are the algebraic sum of two different angles. In trigonometry, finding these angles is a very easy procedure. They can be found using the trigonometric formulas of compound angles. One can find the values of sine and cosine values of the given triangle just by dividing the perpendicular with hypotenuse for sine and hypotenuse with perpendicular for cosine. It is limited up to trigonometry, not involved in geometry and other shapes. Compound angles are found by summing the two angles of the triangles and comparing them with 90°.