Column Matrix

The matrix is a tabular arrangement of numbers, and symbols are of many types. The various types of matrices are differentiated based on their shape, number of rows, number of columns present, etc. The type of matrices includes triangular matrices, row matrices, and column matrices. A column matrix is a type of matrix that contains only one column in it. A column matrix can have only one row. However, it can have many rows. Let us study in-depth the column matrix, the column matrix example, and the properties of the column matrix.

Types of matrices

There are various types of matrices based on their properties like the shape of a matrix, the number of elements present in a matrix, the number of rows, and the number of columns. A few types of matrices are given below.

• Square matrix:

A square matrix is a type of matrix in which the number of rows present in the matrix is equal to the number of columns present in that matrix.

• Rectangular matrix:

A rectangular matrix is a type of matrix in which the number of rows is not equal to the number of columns present.

• Row matrix:

In a row matrix, only a single row is present, and there could be any number of columns present.

• Column matrix: 

In a column matrix, only one column is present. Let us study in-depth about the column matrix.

The column matrix

The Matrix, which only has one column and any number of rows, is called a column matrix. Suppose the order of the matrix is m×n, then for a column matrix, the value of n will always be equal to 1.

Hence the order of a column matrix will be m×1, where m can be any positive integer.

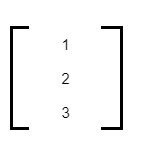
A column matrix example is given below.

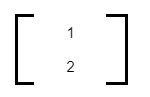
Let us take another example.In the above column matrix, the number of columns present is 1, and the number of rows present is 3.

In this example, the number of columns is still 1 whereas the number of rows is now 2.

You may have noticed from the above examples that the total number of elements in a column matrix is equal to the number of rows in a column matrix. Let us understand what the column space of a matrix is.

The column spaces

The column space of a matrix is also known as the range. The column space of a matrix is the span of its column vectors. This means the column space is a set of all possible linear combinations of its column vectors. 

The column space can be regarded as the range or the image of the corresponding matrix transformations. Any linear combination of the column vectors of a matrix C can be written as the product of C with a column vector.

Let us study the properties of the column matrix.

Properties of a column matrix

Following are the properties of a column matrix.

• The number of columns present in a column matrix is always equal to 1.

• A column matrix can have any number of rows.

• A column matrix is a rectangular type of matrix. This means the number of rows in a column matrix is not equal to the number of rows. 

• The multiplication of a column matrix can only be performed with a row matrix.

• The addition and the subtraction of a column matrix can only be performed with another column matrix of the same order. That is, the number of rows present in both column matrices to be added and subtracted must be equal. 

• A column matrix can only be multiplied with a row matrix, and the product of a column matrix with a row matrix is a singleton matrix.

• The total number of elements in a column matrix is equal to the number of rows present in the column matrix.

Column matrix examples

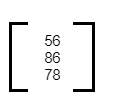
Let us create a column matrix from the given elements. Suppose three elements are to be inserted in a column matrix. The three elements are 56, 86, and 78. Then as our matrix is a column matrix, which means it would only contain a single column, all these elements should be arranged in a single column. 

The number of rows will be equal to the number of elements. The matrix will look like this:

Conclusion:

There are various types of matrices based on the shape, number of rows, columns and the arrangement of the elements in the matrix. The column matrix is also one such type of matrix. A column matrix can contain only one column at maximum; however, it can have any number of rows. Hence the order of the column matrix becomes m×1. The total number of rows present in a column matrix is equal to the total number of elements present in that matrix. A column matrix is a rectangular type of matrix.