Cartesian Coordinate System

In the 17th century, Rene Descartes founded the Cartesian Coordinate system, which revolutionised the mathematics field. The Cartesian Coordinate system is the first system that provided a first systematic link between algebra and Euclidean geometry. The geometrical equations and algebraic equations can be defined by a Cartesian coordinate system which involves the Coordinates of the planes. Cartesian coordinate systems are the foundation of analytical geometry, which interprets many other fields, such as calculus, differential geometry, complex analysis, group theory, and linear algebra. They have a wide range of applications in the mathematical field and various other sectors.

What is the Cartesian Coordinate System?

A Cartesian equation is a coordinate system in a plane with a specific point by a pair of numerical coordinates signed to two fixed perpendicular lines of the same unit length. They consist of reference coordinate lines, and each coordinate reference line is called the coordinate axis. The origin at the ordered pair (0,0) is the point where they meet. In other terms, they are the positions of the perpendicular projections on two axes from the origin. They are the mutually exclusive events that are defined as a three-dimensional space by Cartesian Coordinates and are perpendicular to the planes of the axes.

These are known as hyperplanes.

Types of Cartesian Coordinate System

There are three types of dimensions. They are

• One-dimension

• Two-dimension

• Three-dimensions.

Other than the above dimensions, we have higher dimensions and generalised dimensions.

One dimension of the Cartesian Coordinate System

The coordinate system for a one-dimensional is a straight line with the origin O and a positive and negative side. In one-dimensional, either the plane has a horizontal or vertical line. If the line is plotted horizontally, the right side is taken as positive, and the left side is considered unfavourable. If the line is vertically ordered, then the upper part of the line is positive, and the lower part is negative. Each point on the line concerns the origin and a defined scale. The coordinate of the point is represented as the + or – sign of the numeric value representing its distance from O. Generally, the one-dimensional line is the number line, which can conveniently represent any actual number.

Two-dimensional the Cartesian Coordinate System

The two-dimensional system of the Cartesian Coordinate system is also known as an orthogonal coordinate system and rectangular system. It is an ordered pair of single unit lengths for both axes with an orientation of each axis. The origin turns each axis into a number line. Thus, a point P is drawn perpendicular to each axis where it interests. The two numbers are chosen as the Cartesian Coordinates of P. The first and second coordinates are known as the abscissa and the ordinates of P. Therefore, coordinates are written in two numbers separated by a comma (4 −11.5). Hence the origin includes coordinates (0, 0), and the points on the positive half-axes, one unit away from the origin, have coordinates (1, 0) and (0, 1).

Three-dimensional of Cartesian Coordinate system

A Cartesian coordinate system is a three-dimensional space consisting of triplet lines that pass through an origin. If a point P is considered a hyperplane through a perpendicular, that interprets where that hyperplane cuts the axis as a number. Thus, each pair have a coordinate hyperplane. These hyperplanes are divided into eight planes of trihedral called octants.

The octants are: | (-x,-y,-z) | (+x,+y,-z) | (-x,+y,+z) | (+x,+y,+z) |(+x,-y,-z) |(-x,+y,-z) | (+x,-y,+z) | (-x,-y,+z) |   

Cartesian Coordinate Formula

d = √(x₂-x₁)2 + (y₂+y₁)2

Cartesian Coordinate System Example

Example 1 Show that the coordinate points A(–4,–3), B(3,1), C(3,6), and D(–4,2) form the vertices of a parallelogram. 

Solution 

Let A(–4,–3), B(3,1), C(3,6), and D(–4,2) be the vertices of quadrilateral ABCD. 

Using the distance formula,

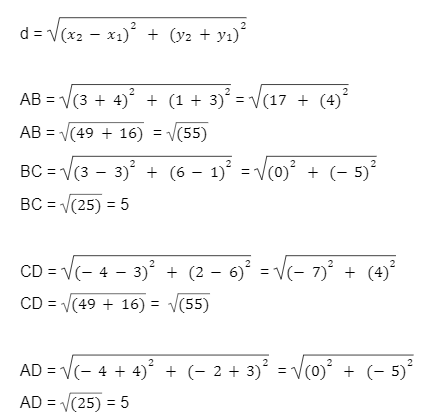
As the opposite sides are equal they form a parallelogram.

Example 2 Calculate the distance between the points A (7, 3) and B which lies on the x-axis whose abscissa is 11.

Solution

The coordinates of B are (11, 0) as the B is on the x-axis, then the y-axis of B is 0.

Using the distance formula the distance between the points A (7, 3), B (11, 0) is

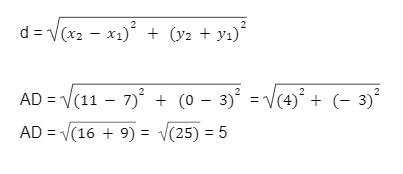
Conclusion

The Cartesian Coordinate is the most familiar concept for graph calculation. It is one of the essential inventions applied in various geometrical sectors including physics, astronomy, and engineering. Most of the systems used in computer programming, computer animations,  and computer-aided designs are employed by this method. Cartesian coordinate systems are the foundation of analytical geometry, which interprets many other fields, such as calculus, differential geometry, complex analysis, group theory, and linear algebra. They are applied in the mathematical field and various other sectors.