Profile
Settings
Refer your friends
Sign out
What are Concurrent Lines?
Three or more lines in a plane passing through the same area are the same lines. Whenever two incompatible lines meet, they form a junction. If the third row also passes where the first two lines meet, then these three lines are said to be the same lines. The intersection of all these lines is called the ‘Consensus Point’. For example, we can see that three triangles are drawn in a triangle crossing a certain area, called ‘Orthocenter’. It should be noted that only unequal lines have a point of alignment as they extend permanently and meet at a certain point.
Concurrent Lines and Concurrency Point
Three or more lines in a plane crossing in one common place are called parallel lines. Two lines on a plane crossing in one place are called cross lines. The common point at which all the same lines meet is called the point of agreement. In the diagram given below, point P is a point of concurrency.
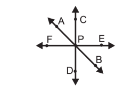
Example 1,
Show that the lines 2a – 3b +4 = 0, 9a + 5b = 19 and 2a -7b + 12 = 0 are compatible. Find a point of agreement.
Solution:
The figures provided are
2a – 3b + 4 = 0 ———- (1)
9a + 5b = 19 ———- (2)
2a -7b + 12 = 0 ———- (3)
By solving the equation 1 and 2, we find
(1) x 5 => 10a – 15b = -20
(2) x 3 => 27a + 15b = 57
—————–
37a = 37
a = 37/37
a = 1
Enter a = 1 in 1 count
2 (1) – 3b = -4
2 – 3b = -4
Remove 2 on both sides.
2 – 3b – 2 = -4 – 2
-3b = -6
Divide by 3 into both sides
b= -6 / (- 3)
b = 2
Thus the point of difference between lines 1 and 2 is (1,2)
Now we have to use a point (1, 2) in the range of 2a -7b + 12 = 0
2 (1) – 7 (2) + 12 = 0
2 -14 +12 = 0
-12 + 12 = 0
0 = 0
From the above statement, we understand that points (1, 2) lies in the third line.
Thus the straight lines are parallel, and the point of consensus is (1, 2).
More than two lines pass through a point. A few examples are the diameters of a circle are concurrent at the centre of the circle. In quadrilaterals, the line segments join midpoints of opposite sides, and the diagonals are concurrent.
Example 2: Make sure that the third row passes where the first two lines meet. The three-line number is 3a + 2b – 15 = 0, a-2b = -3, 4a + 5b – 27 = 0.
Solution:
To test whether the third line passes through the first two lines, we begin by solving the first two numbers.
3a + 2b – 15 = 0 ——- (1)
a-2b + 3 = 0 ——- (2)
4a + 5b – 27 = 0 ——- (3)
In equation (2) we can find the value of 2y.
a – 2b + 3 = 0
Therefore, -2b = -3 -a
2b = 3 + a
Substituting the value of 2y in the equation (1) we receive,
3a + 3 + a – 15 = 0
4a + 3 – 15 = 0
4a – 12 = 0
a = 3
Subtracting the value of ‘x’ in measure (2), we get,
3 – 2b + 3 = 0
6 – 2b = 0
6 = 2b
b = 6/2
b = 3.
Now, we change the values ’x’ and ‘y’ in the scale (3) to check whether they are passing this point and make sure they are along the same lines.
4a + 5b – 27 = 0 ——- (3)
4 (3) + 5 (3) – 27 = 0
12 + 15 – 27 = 0
27 – 27 = 0
Therefore, the three lines are parallel.
Method 2:
To test whether the three lines are parallel, we first find the point of the crossing of the two lines and then check to see if the third line passes through the junction. This will ensure that all three lines are the same. Let’s better understand this by example. The figures for any three lines are as follows.
4a – 2b – 4 = 0 —– (1)
b = a + 2 —– (2)
2a + 3b = 26 —– (3)
Step 1: To find the point of the difference in line 1 and line 2, solve the numbers (1) and (2) in the form of substitution.
Substituting the value of ‘y’ on the scale (2) on the scale (1) we receive,
4a – 2 (a + 2) – 4 = 0
4a – 2a – 4 – 4 = 0
2a – 8 = 0
a = 8/2
a = 4.
To change the value ‘a = 4’ to the scale (2), we get the value ‘y’.
b = a + 2 —– (2)
b = 4 + 2
b = 6
Thus, lines 1 and line 2 intersect at some point (4,6).
Step 2: Substitute the point of intersection of the first two lines on the scale of the third line.
The third row number is 2a + 3b = 26 —– (3)
To change the values of (4,6) in equation (3), we find,
2 (4) + 3 (6) = 26
8 + 18 = 26
26 = 26
Conclusion
We have learned about concurrent lines and listed the difference between concurrent lines and intersecting lines. We also learnt the condition for three lines to be concurrent.
