Profile
Settings
Refer your friends
Sign out
A quadratic equation can be defined as an equation with the highest degree of two. The term “quadratic” is obtained from the term “Quad” and the meaning of the term is square. There are mainly three types of quadratic equations such as vertex form, factored form as well as standard form. The article is going to focus on the description of a quadratic equation as well as the condition for common roots. This equation primarily has two roots and the root’s nature can be imaginary or real. The roots or solution of the quadratic equation is (, ) = [-b √(b2 – 4ac)]2a.
Overview of Quadratic Equations
A quadratic equation can be defined as an algebraic expression of second degree in x and the standard form of this equation is ax2 + bx + c = 0. In this case, x is variable, c is constant, and b and r are the coefficients. Quadratic equations need to have a common root and it needs to be solved by the application of appropriate formulas.
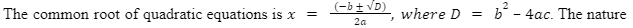
- D>0, thus roots are distinct and real (unequal)
- D<0, thus roots are unequal and imaginary
- D=0, thus roots are equal and real
The roots (α – iβ), (α + iβ) are adjacent pairs. The products and roots of quadratic equations are, in case β and α are the quadratic equations roots. Thus
P = αβ = c/a = constant term/coefficient of x2
S = += -b/a = coefficient of x/coefficient of x2
The Quadratic equations need to have a common root. Thus, then the condition is
There are mainly three forms in the quadratic equations such as:
- Standard form: y = ax2+ bx + c, in which c, b, and a are members.
- Vertex form: y = a(x + b)2+ c, in which c, b, and a are members.
- Factored form: y = (ax + c)(bx + d) , in which d, c, b, and a are members.
Condition for Common Roots
An algebraic polynomial is an algebraic expression that effectively involves terms in the form of cxn, in which the nature of n is non-negative. On the question regarding how to check whether two quadratic equations have common root, then the effective condition is (a1/ a2) = (b1 / b2) = (c1 / c2).
As an example on the description of common roots:
Consider a1x2 + b1x + c1 = 0 and a2x 2+ b2x + c2 = 0 as two quadratic equations
Consider α as the common root in the quadratic equations.
Thus, a22 + b2 + c2 = 0 and a12 + b1 + c1 = 0
The condition for one common root is (c1a2 – c2a1)2 = (b1c2 – b2c1) (a1b2 – a2b1)
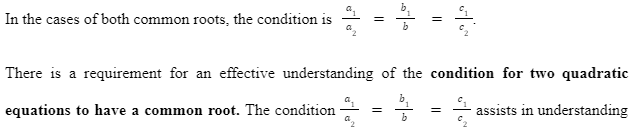
the question of how to check whether two quadratic equations have common root. Here the root is considered as the value of a given variable, where in a quadratic equation it is considered to be x.
Conclusion
Based on the above discussion it can be concluded that quadratic is obtained from the term “Quad” and the meaning of the term is square. There are multiple applications of quadratic formulas such as formulating speed or calculating areas. The article focused on the description of a quadratic equation as well as the condition for common roots. On the uncertainty regarding the Quadratic equations that need to have a common root, the condition (a1/ a2) = (b1 / b2) = (c1 / c2) assists in developing certainty.
