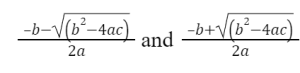A Short Note on Quadratic Equations

The quadratic equation contains one term, which is used for finding solutions and for defining the functions of the polynomials of the degree in 2nd. The equation comes up with a formula that helps to define the functions of the equations and helps to find out the solutions. The variable related to the algebraic expression helps to find out the coefficients and changes the quality of the equation based on the equation. The quadratic equation indicates the exponent of the quadratic and involves highlighting the quality outcome based on the establishment of the values.     

Knowing the Primary Concepts about Quadratic Equation

The standard equation related to the quadratic equation intensifies the generic established of the formula. The term ‘quadratic’ has come from the term quadratus and it means square. The equation indicates the scenarios in which the quadratic degrees are used and that intensifies the quality establishment of the equations. The quadratic equation is a process that forms the formula ax²+ bx+c=0. In this formula the value has differences and the specific measurements are a>0 and there a, b, c is the quadratic equation that is dependent on the rearrangement of the integral values.  

Standard Form of Quadratic Equation

The standard form of quadratic equation comes in different forms and the outcome indicates the value presentation based on the presentation of the formula. The process could be simplified from the outer force of the disguised form in the solutions. For example, if some formulas are disguised in a form of x²=3x-1 then the standard form of quadratic equation will be x²-3x+1=0 in which a, b, and c are respectively 1,3, and 1. Similarly, the other formation pf this quadric equation can be shown as 2(w² – 2w) = 5 can be presented as the standard form of 2w²-2w-5=0 ; here a, b, and c is respectively 2,-4,-5. In the standard form of quadric equation highest value of x’s power will be always  2.      

Formula for Roots of Quadratic Equation

As the quadric equation is a formation where variable x has the highest power of 2, has through driving that equation one can narrow down the value of x, which represented as the root of that quadric equation. The formula for roots of quadratic equation represents the isolation process of the values and with the mathematical proof, the roots of the equations can be analyzed and presented. Based on the formula for roots of quadratic equation the presentation of the formula could be initiated as the generic formulation of the second-degree equation. The basic formula used for the scenario is ax²+bx+c=0 and the other formulas are X can be presented , which means through putting the real value of a, b, c one can drive the value of variable x. 

Conclusion

The quadratic equation is a formative process in algebra that indicates the establishment of the second degree in the value of the x. The quadratic equation indicates the equation format that is ideal to present the formulation presentation of the mathematical equations. The value establishment and finding out the quality enforcement of the values and the process of finding out the root values that indicate the identification of the integral values. Based on the formula the identification of the values is initiated and the formula for roots of quadratic equation indicates the ultimatum of the value 0.