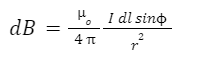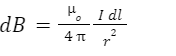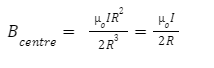Biot Savart’s Law and it's applications- Unacademy

Biot Savart’s Law is the fundamental of magnetostatics. Therefore, it plays a crucial role in the field of electromagnetism. The law describes the equation between the magnetic field produced due to the flow of a constant electric current. The law is useful for knowing the magnetic field’s direction, length, and magnitude, and the proximity of the electric current. It can also be seen as a real-time example of a line integral.

Biot Savart’s Law and Current Loop

Biot Savart’s Law helps to calculate the resultant magnetic field B at position r in the three-dimensional space. The magnetic field is generated due to a flexible wire, which carries current. The steady current in the wire is the continual flow of charge, which does not change with time. Also, the charge neither depletes nor accumulates at any point. The equation of the Biot Savart law is given as,

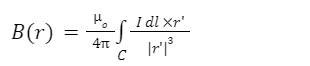
Where

dl represents the vector along which the path C and the magnitude of this vector is the length of the differential of the wire’s element in the direction of conventional current;
‘l’ represents the point on path C. r’ represents the displacement vector from the element of the wire (dl) at point l to the point at which the field is needed to be computed (r), and it is the difference between r and l;
And 𝜇o is the magnetic constant.

The equation can also be written in the form,

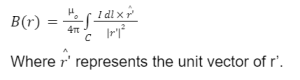
Usually, around a close curve, the integral is found. The reason for this is that the stationary electric current can only travel across a closed path when they are bounded.

Biot Savart’s Law’s Application

A few of the applications of the Biot Savart’s Law are:

To calculate the magnetic field in an indefinitely long straight wire owing to a constant current,
To calculate the magnetic field in the centre of a current-carrying arc,
To calculate the force between two parallel and lengthy current-carrying conductors,
To calculate the magnetic field along the axis of a circular current-carrying coil.

Biot Savart’s Law for a circular current-carrying coil

Assume a circular coil that is carrying current I and has the radius R. Now, if there is a point P that has a distance of x units from the centre of the axis and lies on the axis of the coil. Further, in order to calculate the field around the point P, consider an element of current at the top of the coil Idl. such that the element is pointing perpendicular towards the reader. The vector that is joining the current element and point P is ‘r’.

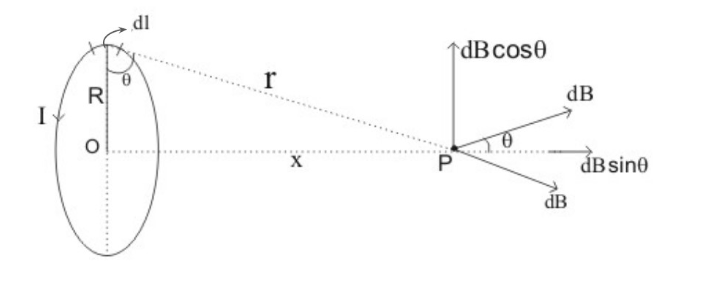
Magnitude of the Field

Using Biot Savart’s Law, the magnitude of the magnetic field generated because of the presence of the current element at P can be written as,
As the element, Idl and r are perpendicular to each other and the value of ϕ is 90o. Therefore, the magnitude can be written as,
Dividing dB into two components — dBsinθ, which is along the loop’s axis, and dBcosθ, which is perpendicular to the horizontal axis.
As the coil is symmetrical about the horizontal axis, the vertical component will be cancelled out because of the presence of another element on the other side of the coil.
The resultant B of the complete loop can be written as,

Direction of B

The magnetic field at a location on a circular coil’s axis is along the axis, and its orientation may be determined using the right-hand thumb rule. The extended thumb will point towards the magnetic field if the fingers are folded along the current.
For anti-clockwise current, the magnetic field will be out of the page, while for clockwise current, it will be on the page.

Field of the coil at its centre (when x=0)

The field at the centre of the coil, where the value of x is 0, can be written as,

Field of the coil that is far from the centre (when x>>>>R)

As the value of x will be much more than R, the value of R can be neglected as compared to x. Therefore, the value can be written as,

Conclusion

Biot Savart’s Law is the fundamental of magneto-statics. The law helps to calculate the resultant magnetic field at some position in the three-dimensional space. The law is only applicable to steady current. Therefore, the flow of charge should continue and must not change with time. The law helps to calculate the magnetic field in a straight or circular coil and to calculate the force between two parallel and lengthy current-carrying conductors.

Also see:

NEET Question Paper	NEET 2021 Question Paper	NEET Books
NEET 2020 Question Paper	NEET 2022 Syllabus	NEET Preparation Tips
NEET Full Form	NEET Preparation Tips by Toppers	How to Prepare for NEET

Important Links:

How Many Hours to Study for NEET	Best NEET Online Coaching App
NEET Preparation Tips by Toppers	NEET Rank Predictor
How to Prepare for NEET From Class 11	NEET 2018 Question Paper
Handwritten NEET Notes	NEET 2021 Question Paper With Solutions