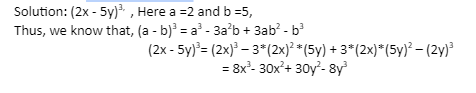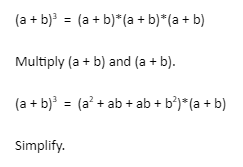(a+b)^3

Algebra is essentially the practice of performing arithmetic-like operations with non-numerical mathematical objects. However, until the nineteenth century, algebra was primarily concerned with the theory of equations. The fundamental theorem of algebra, for example, belongs to the theory of equations and is no longer considered to be part of algebra.

Mathematical operations and formal manipulations are done to abstract symbols rather than concrete integers in algebra. The idea of such a unique subdiscipline of mathematics, as well as the term algebra to describe it, arose from a long and winding historical process. The growth of the concept of the equation, number systems, symbols for expressing and manipulating mathematical propositions, and the modern abstract structural perspective of algebra are all traced in this article. See elementary algebra, linear algebra, and modern algebra for more information on specific branches of algebra, there are many important formulas in algebra that we use every day, one of them is (a – b)3 or (a + b)3 formula.

To find the cube of a binomial, use the (a + b)3 formula. This formula can also be used to factorise certain trinomials. One of the algebraic identities is this formula. The cube of the difference of two terms is calculated using the (a-b)3 formula. This formula is used to quickly and conveniently determine the cube of the difference of two terms without having to perform difficult calculations. Let’s learn more about the (a-b)3 formula and look at several examples with solutions.

Let us Understand how to Evaluate, The (M-N)3 formula is used to calculate the cube of a binomial. The formula is also known as the cube of the difference between two terms. To find the formula of (M-N)3, we will just multiply (M-N) (M-N).

(M – N)3 = (M – N)(M – N)(M – N)

 = (M2 – 2MN + N2)(M – N)

 = M3 – M2N – 2M2N + 2MN2 + MN2 – N3 

 = M3 – 3M2N + 3MN2 – N3 

 = M3 – 3MN(M-N) – N3 

Therefore, (M-N)3 formula is:

(M – N)3 = M3 – 3MN(M-N) – N3 

Uses of (a – b)^3

• Expansion: The subtraction of three times the product of both terms and the subtraction of the second term from the first term, from the subtraction of the cube of the second term from the cube of the first term, expands the cube of difference between any two terms.

(M – N)3 = M3 – 3MN(M-N) – N3

• Simplification: The cube of difference between any two terms is simplified by subtracting three times the product of both terms and subtracting the second term from the first term by subtracting the cube of the second term from the cube of the first term.

M3 – 3MN(M-N) – N3 = (M – N)3