Wave FormulaElectromagnetic wave equations are given as below | ||
| Description | Formula | |
| Gauss’s Law for electricity | ∮ E.da=Q/ϵ_0 | |
| Gauss’s Law for Magnetism | B.dA=0 | |
| Faraday’s Law | E.dl=-dϕdt | |
| Ampere-Maxwell Law | ∮ B.dl=μ_0 ϵ_0 (dϕ_E)/dt | |
| Speed of Light in Vacuum | c=1/√(μ_0 ϵ_o ) | |
| Speed of light in medium | v=1/√μϵ | |
| Relation between Electric and Magnetic field | E_0/B_0 =c | |
Wave FormulaThe formula for wave are as stated below | ||
| Description | Formula | |
| General Equation of Wave Motion | (∂^2 y)/(∂t^2 )=v^2 (∂^2 y)/(∂x^2 ) | |
| Wave number | 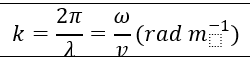 | |
| Phase of a Wave | It is the difference in phases of two particles at any time t. ∆ϕ=2π/λ∆x | |
| Speed of Transverse Wave Along a String / Wire | v=√(T/μ) where T=Tension(-1) μ=mass per unit length | |
| Power Transmitted Along The String By a Sine Wave | Average Power (P) P=2π^2 f^2 A^2 μv v =velocityIntensity I=P/S=2π^2 f^2 A^2 ρv | |
| Longitudinal Displacement of Sound Wave | ϵ=A sin(ωt-kx) | |
| Pressure Excess during travelling sound wave | P_ex=-B ∂ϵ/∂x=(B) Cos (ωt-kx) Where B is the Bulk Modulus Pex is the excess pressure | |
| Speed of Sound | C=√(E/ρ) Here, E is elastic modulus ρ is the density of medium | |
| Loudness of Sound | 10 ( I/I_0 ) dB | |
| Intensity at a distance r from a point Source | I=P/(4πr^2 ) | |
| Interference of Sound Wave | P_1=P_m1 Sin(ωt-kx_1+θ_1 ) P_2=P_m2 Sin(ωt-kx_2+θ_2)The Result is the sum of all the pressure. P_0=√(p_(m_1)^2+p_(m_2)^2+2p_(m_1 ) P_m2 cosϕ) | |
| For constructive Interference | ϕ=2πn then,=>P_o=P_(m_1 )+P_(m_2 ) | |
| For destructive interference | ϕ=(2n+1)π and=>P_o=|P_(m_1 )-P_(m_2 ) | | |
| Close Organ Pipe | f=v/4l,3v/4l,5v/4l,….((2n+1)v)/4l | |
| Open organ pipe | f=v/2l,2v/2l,…nV/2l | |
| Beats | Beats Frequency=f1–f2 | |
| Doppler’s Law | The Observed Frequency, f^’=f((v-v_0)/(v-v_s ))Apparent Wavelength, λ^’=λ((v-v_s)/v) | |
Wave Optics FormulaThe formula for wave optics are as stated below | ||
| Description | Formulas | |
| The path difference of two coherent Waves | ∆d=d2–d1 ∆d is the path difference | |
| The Path difference of two coherent waves: Interference Maximum | ∆d=k.λ ∆d is path difference λ is the wavelength | |
| The path difference of two coherent waves: Interference Minimum | ∆d=((2.k+1).λ)/2 ∆d is path difference λ is the wave length | |
| Thin-film interference: Constructive (maximum) | 2ntcos r =(n+1/2)λ t is film thickness n is refractive index r is refraction angle λ is wave length | |
| Thin-Film interference: destructive (minimum) | 2ntcosr =nλ t is film thickness n is refractive index r is refraction angle λ is wave length | |
| Radii of Newton’s Ring | r=√(k.R.λ) or r=√(((2.k+1).R.λ) )/2 r is the radius R is the radius of curvature λ is the wavelength | |
| Light Diffraction | l=d^2/(4.λ) I is the distance from obstacle d is the obstacle size λ is wavelength | |
| Diffraction grating: maximum (bright stripes) | dsinθ =kλ d is the lattice constant is the diffraction angle λ is the wavelength | |
| Diffraction grating (dark stripes) | dsinθ =(K+1/2)λ d is the lattice constant is the diffraction angle λ is the wavelength | |
Work Power and Energy FormulaThe formula for work power energy are as stated below | ||
| Description | Formulas | |
| Work done is given by | W=F×d F is the force d is the displacement | |
| Kinetic Energy | K.E=1/2 mv^2 m is the mass of the body. v is the velocity of the body | |
| Potential Energy | P.E=mgh m is the mass of the body in kg h is the height of the body in meters g is the acceleration due to gravity | |
| Power | P=W/t W is the work done by the body t is the time P=(F ⃗.(ds) ⃗)/dt=F ⃗.V ⃗ | |
| Conservative Forces | F=-du/dr | |
| Work-Energy theorem | W_net=∆K Where Wnet is the sum of all forces acting on the object K is the change of kinetic energy | |
Kinetic Theory FormulaThe formula for kinetic theory are as stated below | ||
| Description | Formula | |
| Boltzmann’s Constant | k_B= nR/N kB = Boltzmann’s constant R = gas constant n = number of moles N = number of particles in one mole | |
| Total translational Kinetic Energy of Gas | K.E = 3/2 (nRT) R = gas constant n = number of moles T = absolute temperature | |
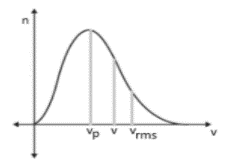
| Maxwell distribution law | V_rms Vp = most probable speed V = average speed | |
| RMS Speed | V_rms= √(3kt/m) = √(3Rt/M) R = universal gas constant T = absolute temperature M = molar mass | |
| Average Speed | v ⃗=√(8kt/πm) = √(8Rt/πM) | |
| Most probable speed | v_p=√(2kt/m) = √(2Rt/M) | |
| Pressure of ideal gas | p = 1/3 ρ〖v^2〗_rms | |
| Equipartition of energy | For each degree of freedom K=1/2 k_B TFor f degree of freedom K=f/2 k_B TkB = Boltzmann’s constant T = temperature of gas | |
| Internal Energy | For n moles of an ideal gas, internal energy is given as U=f/2 (nRT) | |
Kinetic Theory of Gases FormulaThe formula for kinetic theory of gases are as stated below | ||
| Description | Formulas | |
| Boltzmann’s Constant | k_B=nR/N
| |
| Total Translational K.E of Gas | K.E=(3/2)nRT
| |
| Maxwell Distribution Law | V_rms>V>Vp
| |
| RMS Speed (Vrms) | V_rms=√(8kt/m)=√(3RT/M)
| |
| Average Speed | v ⃗=√(8kt/πm)=√(8RT/πM) | |
| Most Probable Speed (Vp ) | V_p=√(2kt/m)=√(2RT/M) | |
| The Pressure of Ideal Gas | P=1/3 V_rms^2
| |
| Equipartition of Energy | K=1/2 K_B T for each degree of freedom K=(f/2) K_B T
| |
| Internal Energy | U=(f/2)nRT
| |
JEE Physics Important Formulas Part -7
In this article, we will go through physics quick formula revision for JEE. Find the important formulas of Wave and Wave Optics, Work Power and Energy, Kinetic Theory and Kinetic Theory of Gases.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out