JEE Maths Formulas – Part 3

Inverse Trigonometric Functions formula

The formula for inverse trigonometric functions are as stated below

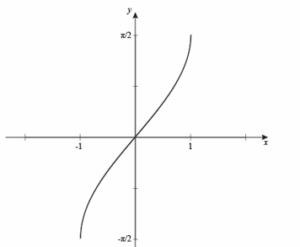
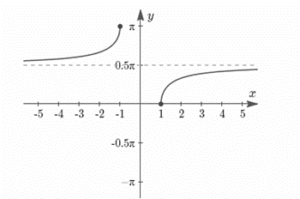
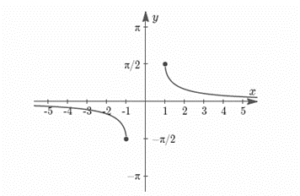
Arcsine function is an inverse of sine function which is denoted by sin^-1

The formula for arcsin is given as

sin^-1(-x)=-sin^-1(x), x∈[-1, 1]

Domain of arcsin is -1≤x≤1

Range of arcsin is -π/2≤y≤π/2

Differentiation of sin^-1x is 1/√(1-x^2 )

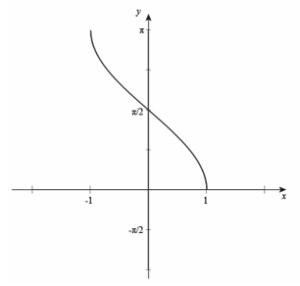
Arccosine function is an inverse of cosine function which is denoted by cos^-1

cos^-1(-x)=π-cos^-1(x), x∈[-1, 1]

Domain of arccos is -1≤x≤1

Range of arccos is 0≤y≤π

Differentiation of cos^-1x is –1/√(1-x^2 )

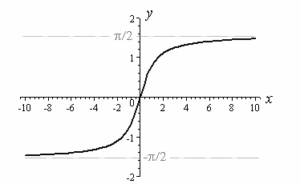
Arctangent function is an inverse of tangent function which is denoted by tan^-1

tan^-1(-x)=-tan^-1(x), x∈R

Domain of Arctangent is -∞≤x≤∞

Range of Arctangent is -π/2≤y≤π/2

Differentiation of tan^-1x is 1/(1+x^2 )

Arc cotangent function is an inverse of cotangent function which is denoted by cot^-1

cot^-1(-x)=π-cot^-1(x), x∈R

Domain of Arc cotangent is -∞≤x≤∞

Range of Arc cotangent is 0≤y≤π

Differentiation of cot^-1x is –1/(1+x^2 )

Arc secant function is an inverse of cosine function which is denoted by cot^-1

sec^-1(-x)=π-sec^-1(x), |x|≥ 1

Domain of Arc secant is -∞≤x≤-1 or 1-∞≤x≤-∞

Range of Arc secant is 0≤y≤π, y ≠π/2

Differentiation of sec^-1x is (-1)/(|x| √(x^2-1))

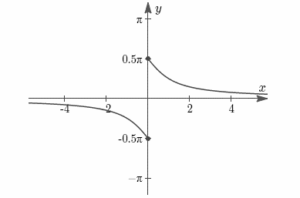
Arc cosecant function is an inverse of sine function which is denoted by cosec^-1

cosec^-1(-x)=-cosec^-1(x), x≥ 1

Domain of Arc cosecant is -∞≤x≤-1 or 1-∞≤x≤-∞

Range of Arc cosecant is -π/2≤y≤π/2, y ≠0

Differentiation of cosec^-1(x) is (-1)/(|x| √(x^2-1))

Straight Line Formula

The formula for straight line are as stated below

Centroid G((x_1+x_2+x_3)/3 ,(y_1+y_2+y_3)/3)

In center I(ax_1+bx_2+cx_3)/(a+b+c),(ay_1+by_2+cy_3)/(a+b+c)

Excentre I1(-a_x+bx_2+cx_3)/(-a+b+c),(-ay_1+by_2+cy_3)/(-a+b+c)

Line Joining two points (x_1 y_1 ) |&(x_2 y_2) |

If is the acute angle between the pair of straight lines, then tanθ

ax+bx+c=0 and a’x+b’y+c’=0 Two lines

1. Parallel if a/a’=b/b’c/c’
2. Distance between two parallel lines= |(C_1-C_2)/√(a^2+b^2 )| 
3. Perpendicular: if aa’+bb’=0

1. Distance between point and line=|(ax_1+by_1+c)/√(a^2+b^2 )| 
2. Reflection of a point about a line:

1. Foot of the perpendicular from a point on the line is

Indefinite Integration formula

The formula for indefinite integration  are as stated below

f(x)dx=gx+c⟺ddxgx+c=f(x)

Here, c is called the constant of integration

• ∫ (ax+b)^n dx=(ax+b)^(n+1)/a(n+1) +c,n≠-1
• ∫ dx/(ax+b)=1/a □ln ln (ax+b) +c
• ∫ e^(ax+b) dx=1/a e^(ax+b)+c
• ∫ a^(px+q) dx=1/P a^(px+q)/(□ln ln a )+c , Here a>0
• ∫ sin (ax+b)dx =-1/a □cos cos (ax+b) +c
• ∫ sin (ax+b)dx =-1/a □cos cos (ax+b) +c
• ∫ tan (ax+b)dx =1/a □ln ln □sec sec (ax+b) +c
• ∫ cot (ax+b)dx =1/a □ln ln □sin sin (ax+b) +c
• ∫(ax+b)dx =1/a tan (ax+b) +c
• ∫(ax+b)dx =-1/a cot (ax+b) +c
• ∫(ax+b)dx =-1/a cot (ax+b) +c 

or∫ dx =ln tan (π/4+x/2)+c

• ∫ dx =ln (x +cot x ) +c or ∫ dx =ln tan x/2 + c
• ∫ dx =ln (cosec x+cot x ) +c
• ∫ dx =ln (cosec x+cot x ) +c
• ∫ dx/(a^2+x^2 )=-1/a x/a +c
• ∫ dx/(|x| √(x^2+a^2 ))=-1/a x/a +c
• ∫ dx/√(x^2+a^2 )=ln [x+√(x^2+a^2 )] +c
• ∫ dx/√(x^2-a^2 )=ln [x+√(x^2-a^2 )] +c
• ∫ √(a^2-x^2 ) dx=x/2 √(x^2+a^2 )+a^2/2 x/a +c
• ∫ √(x^2+a^2 ) dx=x/2 √(x^2+a^2 )+a^2/2 ln ((x+√(x^2+a^2 ))/a) +c
• ∫ √(x^2-a^2 ) dx=x/2 √(x^2-a^2 )-a^2/2 ln ((x+√(x^2-a^2 ))/a) +c

Make the substitute x+b2a=t

∫ dx/(a+bx ) or∫ dx/(a+bx )   or∫ dx/(ax +b□sin sin x □cos cos x +cx )

Here we put tan x =t

Here we put tan x/2 =t

Here k is any constant

So, we divide numerator and denominator by x^2 and put x∓1/x=t

Application Of Derivatives formula

The formula for application of derivatives are as stated below

• Tangent at(x_1,y_1) is given by(y-y_1 )=f^’ (x_1 )(x-x_1 ), here the f'(x_1) should be real
• And normal at(x_1,y_1) is given by(y-y_1 )=-1/(f^’ (x_1 ) )(x-x_1), here the f^’ (x_1 ) should be non-zero and real.

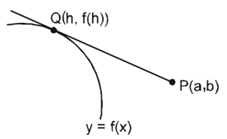
Given a point P(a, b) which does not lie on the curve y = f(x), then the equation of possible tangents to the curve y = f(x), passing through (a, b) can be found by solving for the point of contact Q.

And equation of the tangent is

• PT=|k| √(1+1/m^2 ) is the length of the tangent
• PN=|k| √(1+m^2 )  is the length of normal
• TM=|k/m| is the length of the subtangent
• MN=|km| is the length of subnormal

Angle between two intersecting curves is defined as the acute angle between their tangents (or normal) at the point of intersection of two curves. So,

If a function f defined on [a, b] is

• continuous on [a, b]
• derivable on (a, b) and
• f(a) = f(b),
• then there exists at least one real number c between a and b

(a < c < b) such that f’(c) = 0

If a function f defined on [a, b] is

(i) Continuous on [a, b] and  (ii) derivable on (a, b)

then there exists at least one real numbers between a and b (a < c < b) such that

• Volume of a cuboid =lbh
• Surface area of cuboid =2(lb+bh+hl)
• Volume of cube =a³
• Surface area of cube =6a²
• Volume of a cone =1/3 πr^2 h
• Curved surface area of cone =πrl (l=slant height)
• Curved surface area of a cylinder =2πrh
• Total surface area of a cylinder =2πrh+2πr²
• Volume of a sphere =43r³
• Surface area of a sphere =4πr²
• Area of a circular sector =1/2 r^2 θ , here θ is in radian
• Volume of a prism =area of the base×(height)
• Lateral surface area of a prism =perimeter of the baseheight
• Total surface area of a prism =lateral surface area×2(area of the base)
• Volume of a pyramid =1/3area of the base×(height)
• Curved surface area of a pyramid =1/2perimeter of the base×(slant height)