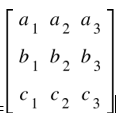Vectors Formula

The formula for vectors are as stated below

If a and b are positive vectors of two points A and B, then

AB =b- a

• Distance Formula: Distance between the two points A( a ) and B( b) is

AB= $|(a)⃗-b⃗|$

• Section Formula: $r⃗=(n(a)⃗+mb⃗)/(m+n)$      Midpoint of AB=$((a)⃗+b⃗)/2$

a .b= a b cosθ , where a , b are the magnitude of a and b respectively and θ is the angle between a and b

• i.i=j.j=k.k=1; i.j=j.k=k.i=0 , projection of a  on b= a . b /b 
• If ( a ) ⃗=a_1 i+a_2 j+a_3 k & ( b ) ⃗=b_1 i+b_2 j+b_3 k then a ⃗.( b ) ⃗=a_1 b_1+a_2 b_2+a_3 b_3
• The angle ∅ between a & b is given by ∅ =〖cos〗^(-1) (a ⃗.( b ) ⃗)/| ( a ) ⃗ || ( b ) ⃗ | ,0≤∅≤π.∅=〖cos〗(−1)(a⃗.(b)⃗)/∣(a)⃗∣∣(b)⃗∣,0≤∅≤π
• a . b =0 a Perpendicular to  b   (a≠0, b ≠0)

• If a & b are two vectors and is the angle between them then
• a. b =absinθ n , where n is the unit vector perpendicular to both a & b such that a,b& n form a right handed screw system

• Geometrically a b=area of the parallelogram whose two adjacents sides are represented by a & b 
• i.i=j.j=k.k=0;  i.j=k,  j.k=i,  k.i=j
•  a ⃗=a_1 i ̂+a_2 j ̂+a_3 k ̂ & b ⃗=b_1 i ̂+b_2 j ̂+b_3 k ̂ then a ⃗× b ⃗= =  b= o↔  a and b are parallel (collinear) (a≠0, b≠0) i.e. a=K b where K is a scalar. $\pm (a⃗\times b⃗)/|a⃗\times b⃗|$

• Unit vector perpendicular to the plane of a & b is n= $ABC=1/2[a⃗\times b⃗+b⃗\times c⃗+c⃗\times a⃗]$
• If a,b & c are the position vectors of 3 points A, B & C then the vector area of triangle ABC=1/2ab+bc+ca. The points A, B & C are collinear if
  • $a⃗\times b⃗+b⃗\times c⃗+c⃗\times a⃗=0⃗$

• Area of any quadrilateral whose diagonal vectors are (d_1 ) ⃗ & (d_2 ) ⃗ is given by 1/2 |(d_1 ) ⃗×(d_2 ) ⃗ |1/2∣(d1)⃗×(d2)⃗∣

• Lagrange’sIdentity:(a ⃗×b ⃗ )^2=|a ⃗ |^2 |b ⃗ |^2-(a ⃗.b ⃗ )^2=[((a) ⃗×a ⃗ ) (a ⃗×(b)) ⃗ ( b ⃗×(a)) ⃗ ( b ⃗×(b)) ⃗](a⃗×b⃗)2=∣a⃗∣2∣b⃗∣2−(a⃗.b⃗)2=[((a)⃗×a⃗)(a⃗×(b))⃗(b⃗×(a))⃗(b⃗×(b))⃗]

• The scalar triple product of three vectors a,b & c  is defined as:

$a⃗\times b⃗.c⃗=|a⃗||b⃗||c⃗|\square sinsin\theta \square coscos\varnothing$

• Volume of tetrahedron $V=[a⃗.b⃗.c⃗]$

• In a scalar triple product the position of dot and cross can be interchanged i.e.

$a⃗.(b⃗\times c⃗)=(a⃗\times b⃗).c⃗Or[a⃗b⃗c⃗]=[b⃗c⃗a⃗]=[c⃗a⃗b⃗]a⃗.(b⃗\times c⃗)=-a⃗.(c⃗\times b⃗)i.e.[a⃗b⃗c⃗]=-[a⃗c⃗b⃗]$

• If a ⃗=a_1 i+a_2 j+a_3 k; b ⃗=b_1 i+b_2 j+b_3 k & c ⃗=c_1 i+c_2 j+c_3 k then

a.b.c=

• If a,b,c are coplanar
  $[a⃗b⃗c⃗]$

• Volume of tetrahedron OABC with O as origin & A(a), B(b) and C(c) be the vertices = $|1/6[a⃗b⃗c⃗]|$

• The position vector of the centroid of a tetrahedron if the pv’s of its vertices are a,b,c & d are given by $1/4[a⃗+b⃗+c⃗+d⃗]$

$a⃗\times (b⃗\times c⃗)=(a⃗.c⃗)b⃗-(a⃗.b⃗)c⃗,(a⃗\times b⃗)\times c⃗=(a⃗.c⃗)b⃗-(b⃗.c⃗)a⃗$

In general: (a ⃗×b ⃗ )×c ⃗≠a ⃗×(b ⃗×c ⃗ )(a⃗×b⃗)×c⃗=a⃗×(b⃗×c⃗)

Parabola formula

The formula for parabola are as stated below

The equation of parabola with focus at (a,0), a>0 and directrix x = -a is given as

y^2=4axy2=4ax

When vertex is (0, 0) then axis is given as

y = 0

Length of latus rectum is equals to 4a

Ends of the latus rectum are L(a, 2a) and L’(a, -2a).

The point (x,y1) lies outside, on or inside the parabola which is given as y = 4ax

Therefore, equation of parabola now becomes,

〖y_1〗^2-4ax≥0〖y1〗2−4ax≥0

Or

〖y_1〗^2-4ax<0〖y1〗2−4ax<0

Length of the chord intercepted by the parabolay^2=4axy2=4ax  on the line y = mx+c is given as

4/m^2 (√(a(1+m^2 )(a-mc) )4/m2(√(a(1+m2)(a−mc))

Tangent of the parabola y^2=4axy2=4axis given as T = 0

y=mx+am , m≠0 is the tangent of parabola y^2=4ax at (a/m^2 ,2a/m)y2=4axat(a/m2,2a/m)

Normal to the paraboly^2=4axy2=4ax is given as

y-y_1=(-y_1)/2a (x-x_1 )y−y1=(−y1)/2a(x−x1)

The equation of the chord of parabola y^2=4axy2=4axwith midpoint (x1, y1) is given as T = S1.

Here,

S_1=y_1-4axS1=y1−4ax

Definite Integration Formula

The formula for definite integration are as stated below

∫_a^b f(x)dx=∑_(r=1)^n hf(a+rh)∫abf(x)dx=∑(r=1)nhf(a+rh)

Here $h=(b-a)/n$

is the length of each subinterval

∫_a^b f(x).dx=∫_a^b f(t).dt∫abf(x).dx=∫abf(t).dt

∫_0^2a f(x).dx=2∫_0^a f(x).dx f(2a-x)=f(x)

∫_a^∞ dx/(x^2+a^2 )=π/2a∫a∞dx/(x2+a2)=π/2a

• ∫_a^∞ (x^m dx)/(x^n+a^n )=(πa^(m-n+1))/(n ((m+1)π)/n) ),0<m+1<n∫a∞(xmdx)/(xn+an)=(πa(m−n+1))/(n((m+1)π)/n)),0<m+1<n
• ∫_a^∞ (x^(p-1) dx)/(1+x)=π/(□sin sin (pπ) ),0<p<1∫a∞(x(p−1)dx)/(1+x)=π/(□sinsin(pπ)),0<p<1
• ∫_a^∞ dx/√(a^2-x^2 )=π/2∫a∞dx/√(a2−x2)=π/2
• ∫_a^∞ √(a^2-x^2 ) dx=(πa^2)/4∫a∞√(a2−x2)dx=(πa2)/4

• ∫_0^π mx )nx )dx={0 if m≠n π/2 if m=n m,n positive integers
• ∫_0^π mx )nx )dx={ 0 if m≠n π/2 if m=n m,n positive integers

• ∫_0^π mx )nx )dx={ 0 if m+n even 2m/(m^2-n^2 ) if m=n odd m,n integers
• ∫_0^(π/2) x dx=∫_0^(π/2) x dx=π/4∫0(π/2)xdx=∫0(π/2)xdx=π/4

• ∫_0^(π/2) x dx =∫_0^(π/2) dx =(1.3.5…….2m-1)/(2.4.6……2m).π/2,m=1,2,…∫0(π/2)xdx=∫0(π/2)dx=(1.3.5…….2m−1)/(2.4.6……2m).π/2,m=1,2,…

• ∫_0^(π/2) x dx =∫_0^(π/2) dx =(2.4.6….2m)/(1.3.5…2m+1),m=1,2,…∫0(π/2)xdx=∫0(π/2)dx=(2.4.6….2m)/(1.3.5…2m+1),m=1,2,…

• ∫_0^nT f(x)dx=n∫_0^T f(x)dx,n∈z,∫_a^(a+nT) f(x)dx=n∫_0^T f(x)dx,n∈z, a∈R∫0nTf(x)dx=n∫0Tf(x)dx,n∈z,∫a(a+nT)f(x)dx=n∫0Tf(x)dx,n∈z,a∈R

• ∫_mT^nT f(x)dx=(n-m)∫_0^T f(x)dx,m,n∈z,∫_nT^(a+nT) f(x)dx=∫_0^a f(x)dx,n∈z, a∈R∫mTnTf(x)dx=(n−m)∫0Tf(x)dx,m,n∈z,∫nT(a+nT)f(x)dx=∫0af(x)dx,n∈z,a∈R
• ∫_(a+nT)^(b+nT) f(x)dx=∫_a^a f(x)dx,n∈z, a,b∈R∫(a+nT)(b+nT)f(x)dx=∫aaf(x)dx,n∈z,a,b∈R

Ellipse Formula

The formula for ellipse are as stated below

x^2/a^2 +y^2/b^2 =1, where

• Eccentricity: e=√(1-b^2/a^2 ) (0<e<1)  Directrices: x=±a/e
• Foci: S=±a e,0. Length of major axes =2a and minor axes =2b

• Vertices: A’=-a,0 & A=a,0.

• Latus Rectum: = (2b^2)/a=2a(1-e^2)

Auxiliary circle

Parametric Representation

Position of a Point w.r.t. an Ellipse

The point P(x_1,y_1) lies outside, inside or on the ellipse according as;

Line and an Ellipse

Tangents

• Slope form: y=mx±√(a^2 m^2+b^2 )
  ,  point form: 〖xx〗_(1 )/a^2 +〖yy〗_1/b^2 =1

• Parametric form: xcosθ/a+ysinθ/b=1

Normal

Director Circle