In geometry, Circle is an important shape for the students in Mathematics. The application of the Circle in many parts of science such as Mathematics, Physics and Astronomy are based on the theoretical importance of the circle. Circle is a curved line that has an equal interval from the focal point and is connected to the starting point.
On the other hand, Circle is a locus of every point that has the same distance from the center. It is a unique type of ellipse in that its foci are coincident and its eccentricity constant. The radius of the circle is a curved line from the origin to the outer side of the circle. The diameter of the circle is a curved line that divides the whole circle into two same sectors and the length of the diameter is always twice its radius.
Definition of circle
Circle is a two dimensional shape that is evaluated on the basis of the radius of the circle. Quarter circle is formed by the splitting of any circle into four same sectors and this type of circle is known as quadrant. Diameter of the Circle is a longest chord that touches the outside of the circle and crosses through the origin of the circle.
The interval between the circumference and origin is known as a radius of the circle. Its length is a half of the diameter. The total interval around the entire circle is called the circumference and it is also called the arc length or perimeter of that circle. Tangent of the circle is defined as a straight line that passes through all the common points of the circle. Consider a circle of diameter AB and the tangent is MN with circumference of C and origin O.
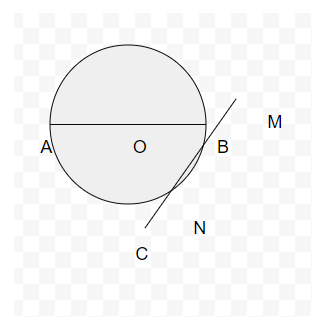
Different types of circle
There are mainly two types of circles; one is the tangent circle and the other is the concentric circle. Tangent circles are denoted as curved lines that intersect or pass through a particular point of the circle. General equation of the tangent circle is a2 +b2=x2 at (xCosθ, xSinθ) that is aCosθ+ bSinθ= x. The condition of the tangent circle is when the particular point lies inside the circle, the point lies on the circle and the point lies outside the circle gives the chance of tangency to the circle for becoming a tangent circle.
On the other hand, the concentric circle is defined as the same or equal origin base circle which means two circles have identical middle points. The region in between two concentric circles has separate radii; it’s called an annulus. Consider, the mathematical statement of the circle is a2+ b2+ 2ga+ 2fb+ k= 0. Where k is constant, the origin of the circle is (-g,-f) and the radius of the circle is (g2+f2-k).
Again, let the mathematical statement of the other circle concentric with the first circle is a2+b2+ 2ga+2gb+kc= 0. It is shown that two different circles have the same origin (-g,-f) however, the radii of that circle is different, that is k≠kc.
The formula of the circles
A circle has a specific shape and it is denoted by the group of points that lie on a plane that are equidistant from the origin of the circle. The formulas of the circle are mainly generated to determine the diameter, area and perimeter of the circle. The below image shows that the AB is a straight line divided by the circle into two equal parts with the radius r and circumference C.
Formulas for calculating the diameter, area and circumference of the circle is P=2×a, where P is the diameter of any circle and ‘a’ is the radius of that circle. To determine the area of the circle is D= π× a2, where is the radius, D is the area of the circle and π= 22/7. The formula of the circumference of the circle is A=2×π×r. Where A denotes the circumference and r is the radius of the circle.
Properties of the circle
The circle word is taken from the Greek word “Kirkus” which means the hoop or ring. There are several types of properties of the circle in mathematics and its connection with polygons, straight lines and angles shows the various importances in mathematics. Consider a circle with radius O and XY is the chord of that circle; it means ON is perpendicular to XY.
To determine the properties of a circle towards the chord is to prove XN=YN. Let, in the triangle, XON and triangle YON have the radius XO=OY and the sides ON are common sides for both triangles. Therefore, angle XON and angle YON is a right angle that is a 90-degree angle. Again, the triangle XON≃ triangle YON [from the R.H.S congruence rule] and therefore, XN=YN [from CPCT theorem].
Importance of circle
The importance of a circle is mostly calculated in architecture for making highways and houses. It is also used in sports by creating balls for tennis, cricket and football. Circle helps to create the constant “pi”, it is not only a number; it appears randomly in every mathematical context. Another use of the circle is to discover wheels that promote the human’s life to a great level. It is also used to make cars, trains and bikes to keep human life more prominent.
Conclusion
By the diameter the circle was equally divided into two sectors; one was exterior and the other was interior. It was a bounded surface that consists of all equidistant points from the origin and the lines passing through the circle as a form of “line of reflection”. If the angle of a circle is subtended through the chords at the origin of the circle is equal, then the chords are identical.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






