The Concept of Truth of Statement

In computer logic, boolean algebra, and digital electronics among many other fields, we often need to verify the correctness or truth value of a statement. Truth verification takes place usually by using truth values. Boolean logic comes in very handy in several cases where the answer can range only between true or false, there is no other value in between. Read on to know more about logic and how the different logic statements are used. 

What is a Logic?

Logic is an idea or a statement that can be answered with truth values – true or false. Every logic statement can only have two values, and nothing more. They can also be represented using logic gate circuits. 

What is a Logic Gate?

A logic gate is a schematic computational model used to represent boolean logic or statements. These gates usually have one or more inputs but produce only one output. Some popular logic gates used in electronics and computer science include the AND gate, the NAND gate, the OR gate, the NOR gate and the XNOR gate among others.

Truths and Falses

In boolean algebra, computer logic or digital electronics, a particular statement can only hold two possible values – true or false. A statement that is factually correct can have the value True.  On the other hand, incorrect statements can only be False. There is no option in between. For example, the statement “The snail is slow” is true, but the statement “Lions eat grass” is false. 

Popular Logic Statements and Truth Tables

Some popular logic statements used in boolean algebra, computer science and digital electronics are NOT, AND, OR, NOR, NAND, XOR, and XAND. Let us look at each of these logic statements and check out their truth tables and logic gates for greater understanding and clarity on the topic. 

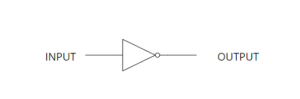
NOT Statement

The NOT statement is used to invert the truth value of a given statement. If the variable is initially true, it becomes false and if it is initially false, it becomes true. The NOT statement takes only one input and has only one output.

NOT Truth Table

NOT Gate

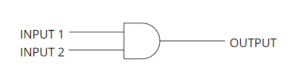
AND Statement

The AND statement is used to check for the validity of two or more statements. If both are true, then the output is true, otherwise, it is false. The AND statement takes more than one input and has only one output.

AND Truth Table

AND Gate

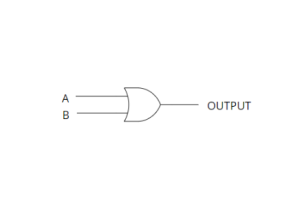
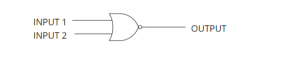
OR Statement

The OR statement is used to check for the validity of any of two or more statements. If at least one statement is true, then the output is true, otherwise, it is false. The OR statement takes more than one input and has only one output.

OR Truth Table

OR Gate

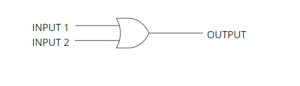
NAND Statement

The NAND statement is used to check for the validity of two or more statements and invert it. If all the input statements are false, then the output is true, otherwise, it is false. The NAND statement takes more than one input and has only one output.

NAND Truth Table

NAND Gate

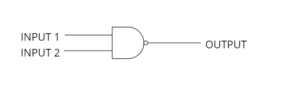
NOR Statement

The NOR statement is used to check for the validity of either two or more statements and invert the truth value. If at least one statement is true, then the output is false, otherwise, it is true. The NOR statement takes more than one input and has only one output.

NOR Truth Table

NOR Gate

XOR Statement

The XOR or exclusive OR statement is used to check the truth value of both statements. If the input statements hold different truth values, whether true or false, then the output is true, otherwise, it is false. The XOR statement takes two inputs and has only one output.

XOR Truth Table

XOR Gate

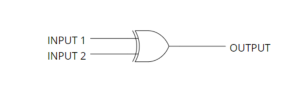
XNOR Statement

The XNOR or Exclusive NOR statement is used to check the truth value of both statements. If both the input statements hold the same value, then the output is true, otherwise, the output is false. The XNOR statement takes two values and gives a single output. 

XNOR Truth Table

XNOR Gate

Conclusion

After going through this topic, you have proper knowledge regarding logic statements and logic gates. To get a better understanding and clarity regarding the use of logic gates, you can practice using logic gates and draw logic gate circuits. There is no better way to understand this topic than constant practice. You would be able to find the implementation of logic gates in several circuits like that of adders, subtractors and multiplexers among others.