Coded Directions Problems

Coded Directions Problems are paragraph-type problems and this topic can be really useful for scoring easy marks. Coded directions relation questions don’t take much time and are not complex. The examiner of the competitive examinations wants to test the students on the basis of direction managing analysis. The coded directions relation questions contain two or more statements, where each statement will ask an individual to move in a particular direction and subsequently new directions are stated in forwarding statements. Each statement will dedicate a new direction and the student has to calculate the final direction where the person is heading. In this article, you’ll learn coded directions in relation question answers.

Coded Directions 

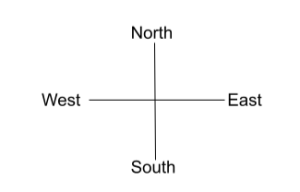
Coded Directions have four major directions. 

The four prominent directions are East, North, South, and West. 

We will use short forms instead of using full names of these directions. E for the east, W for the west, S for the south, and N for the north.

Cardinal Directions

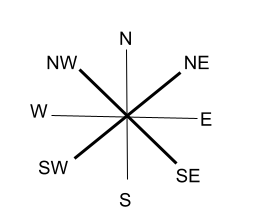
The direction between any two mainstream directions is known as Cardinal Directions.

North-East is denoted by NE, South-East is denoted by SE, South-West is denoted by SW, and North-West is denoted by NW.

Shortest Distance Between Two Points

The shortest distance is also sometimes called displacement between two points. 

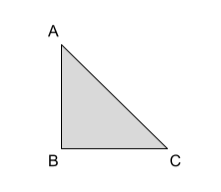
To find the displacement between any two points, we need to remember the Pythagoras theorem because if we join both the points to each other and there will be an origin or junction where the directions meet, all three points will form a right triangle. And, we know that we can apply the Pythagoras theorem only in solving a right-angled triangle.

AB is the perpendicular.

BC is the base 

AC is the hypotenuse

The shortest displacement is AC = square root of (AB2 + BC2).

Coded Directions Relation Questions

Category 1. Based on the final direction

In this category of coded directions relation questions, the questions are mainly about finding out the last position of the person from the initial point after walking or moving in some directions or sub directions.

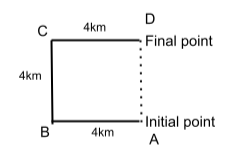
Example 1. After starting from a point, a woman walks 4km towards the west, then turning to her right she moves 4km. After this, she again turns right and moves 4km. Which of the following options here determines the correct direction in which she is from the initial point?

Option a. North

Option b. East

Option c. South

Option d. West

Solution: – We can the optimum solution just by drawing a diagram by following the conditions mentioned in the paragraph.

After analyzing every statement, 

AD is the shortest distance between the starting position and the final position of the woman.

We can derive easily that the woman was heading in the north direction from her starting point.

Option a. North is the correct option.

Example 2. Five villages are situated in close proximity to each other. A is situated to the west of B, C is situated to the south of A, E is situated to the north of B and D is situated to the east of E. Then, in which direction C is with the respect to D?

Option a. North-West

Option b. South-East

Option c. South-West

Option d. Data Inadequate

Example 3. If South-West gets converted into North, then what will be the new North-East be?

Option a. North

Option b. South-East

Option c. South

Option d. East

Solution: – We can clearly observe that the directions are converting 135 degrees in the clockwise direction. Hence, the northeast will convert into the South after moving 135 degrees clockwise.

Solution: – C lies to the South-West of D.

Category 2. Based on Displacement

In this category of coded directions relation questions, we have to find out the final distance between the point where the person started and the point where he stopped his travel.

Example 1. Vijay travelled 12km southward, then turned right and then travelled 10km, then turned right and travelled 12km. How far did Vijay walk away from his starting point?

Option a. 22km

Option b. 44km

Option c. 12km

Option d. 10km

Solution: – The best way to approach this problem is to keep a white sheet just next to yourself and draw out the figure as per the conditions and directions assigned in every statement.

Point A is the starting point and D is the final point of travelling Vijay.

Hence, the distance Vijay has to travel from the starting point is 

AD = BC = 10 km.

Category 3. Based on direction and displacement

In this category of coded directions relation questions, we have to calculate both the displacement along with the direction.

Example 1. Shyam goes 5km in the North from his school. Now, he turns in the left direction and walked 10km and again turns to the left and walks for 5km. How far did he go from his school and also find the direction in which he proceed?

Option a. 10km, South of the school

Option b. 10km, North of the school

Option c. 10km, West of the school

Option d. 10km, East of the school

Solution: – Let point A be the starting point from where he began his journey, i,e, from the school and point D be the final point where he stopped.

AB = CD = 5 kilometer and AD = BC = 10km.

So, Shyam is 10km far away from his school and in the west direction which is also very easy to predict.

Hence, Option c is correct.

Conclusion

The coded directions relation questions contain two or more statements, where each statement will ask an individual to move in a particular direction and subsequently new directions are stated in forwarding statements. Each statement will dedicate a new direction and the student has to calculate the final direction where the person is heading. You learnt how what has coded directions relation questions are answered, and how to solve coded directions relation questions with ease and perfection.