Profile
Settings
Refer your friends
Sign out
A trapezium is a form of a quadrilateral with a closed plane shape consisting of four sides and four corners. The term “Trapezium” is derived from the Greek word “trapeza” which signifies table. According to Euclidean geometry, it is referred to as a type of quadrilateral with two-dimension that has a pair of parallel opposite sides. The parallel opposite sides are known as the base and the non-parallel sides are called legs of the trapezium. The following figure represents a trapezium:
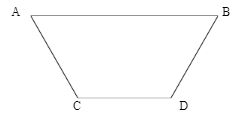
The above figure represents a trapezium with AB and CD as bases while AC and BD as the legs.
Properties of a Trapezium
Properties of trapezium include: –
- Has a pair of parallel sides
- Has a pair of non-parallel sides
- The trapezium is a four-side closed figure with a sum of interior angles equal to 360°
- The sum of exterior angles measures 360°
- At the intersection point diagonals of trapezium bisect each other
- The sum of the angles of adjacent sides is 180°
- It is a 2D shape like a square, rectangle, polygon, etc
- The two non-parallel sides are equal
Shape of Trapezium
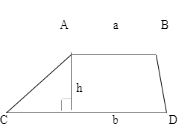
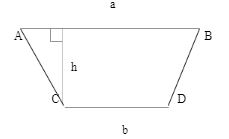
A quadrilateral; is said to be a trapezium when it has a 2-Dimensional closed shape figure with four sides, in which two opposite sides are parallel to each other. The above diagram shows a quadrilateral ABCD, in which AB and CD are parallel to each other but AC and BD are non-parallel, ‘h’ is the height between two parallel lines.
Area of the given trapezium
The area of the trapezium is measured using the length of the sides that are parallel along with the distance (the height) that is between them. The formula for measuring area of trapezium using height and base is
Area (A) = ½ (a+b)* h
Where,
a and b are the bases of trapezium,
h= the shortest distance between the trapezium
Geometrical Properties of a Trapezium:
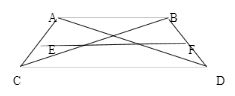
In the above trapezium ABCD,
AB and CD are parallel to each other,
E and F are the middle points of AC and BD respectively.
EF = ½ (AB+CD)
Area of ▲BCD = Area of ▲ACD
Area of ▲ABC = Area of ▲ABD
Types of Trapezium
There are three types of Trapezium:-
- Isosceles Trapezium
- Scalene Trapezium
- Right Trapezium
Isosceles Trapezium
When one talks about the types of trapezium, the first and foremost type that comes to one’s mind is an isosceles trapezium. An isosceles trapezium is also known as an isosceles trapezoid, which has equal base angles. Therefore, the lengths of the left and right sides are equal. Shortly, when the opposite sides of a trapezium are parallel and have two non-parallel sides of the same lengths, the diagonals also measure the same then the trapezium is called an isosceles trapezium. An isosceles trapezium has 4 edges, 4 vertices, and 1 line of symmetry.
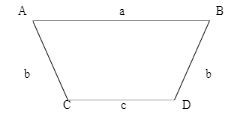
The above figure (ABCD) shows an isosceles trapezium with equal legs,
I.e. AC=BD.
Therefore, the perimeter of an isosceles trapezium is
P= a+b+c+d
P= a+b+b+c
P = a+2b+c.
Scalene Trapezium
A scalene trapezium is a type of trapezium, also known as a scalene trapezoid, in which all four sides and the angles are unequal in length. Scalene trapezium has two parallel sides with two non-parallel sides.
In the above figure (ABCD) of a scalene trapezium:
Sides are unequal AB≠AC≠CD≠BD
Angles are also unequal ∠A≠∠B≠∠C≠∠D
Right Trapezium
The right trapezium is a type of trapezium, which has right angles in a pair that is two angles in a trapezium, is 90°, and has two parallel sides.
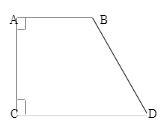
The above figure ABCD is a Right Trapezium where:
Two sides AB and CD are parallel to each other
Two right angles ∠A and ∠C
