Profile
Settings
Refer your friends
Sign out
A power, sometimes known as indices, is a tool for compactly writing a product of integers. Indices are the plural of index. We will go through how to accomplish so in this leaflet and a few rules or laws that may be used to make indices-based statements easier to understand.
The power or exponent that is increased to a value or a variable is known as an index (indices) in mathematics. For example, in number 24, 4 is the index of 2. Indices are the plural of indices. Constants and variables are introduced in algebra. A constant is a value that does not change. On the other hand, a variable quantity can be allocated any number or have its value altered. You deal with indices in terms of sheer numbers in algebra.
For repetitive multiplication, indices give a succinct algebraic notation. It is, for instance, significantly easier to write 96 instead of 9x9x9x9x9x9.
Indices laws emerge naturally when using index shorthand to simplify numeric and algebraic equations. For all positive integers r and t, the simplification of
An Indices can be assigned to a number or a variable. A variable’s Indices (or constant) is a quantity that is lifted to the variable’s power. Indexes are also referred to as powers or exponents. It displays how many times a particular number must be multiplied. It takes the following form:
am = a × a × a ×……× a (m times)
The base is a, and the Indices is m.
The index specifies that a given integer (or base) should be multiplied by an amount equal to the Indices raised to it. It is a shortened way of expressing large numbers and calculations.
Before working with Indices, we must first understand specific fundamental rules or laws that govern them. These rules are applied while conducting algebraic operations on indices and solving algebraic equations, which includes it.
When the intercepts of any other crystal face on the three axes are observed, the following generalizations are seen, which is known as the law of rational indices. Any face of the crystal’s intercepts on the axis of crystallography are either:
(i) The same as the fundamental planes, or
(ii) Multiples of the fundamental plane in simple whole numbers, or
(iii) If the face is parallel to one or both axes, i.eThe face does not cut one or both axes, one or both intercepts must be infinite.
Second Law:
The laws of indices are principles used to alter expressions utilizing indices. Multiplication, division, power of zero, brackets, minus, and fractional powers are all examples of indices laws (also known as indices rules). Do not be tempted to make up your own variants of the rules; they should be followed precisely as written. Here are the three most important laws:
Determine the precise value of t.
8½ x 2t= 4³
Even though the bases appear different, we may rewrite each word to have a base of 2.
Example 2: The coefficient of the bases is one.
Simplify your response and leave it in index form.
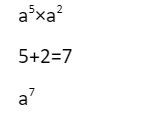
Dividing indices
Subtract the powers when dividing Indices with the same base.
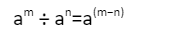
What does it mean to divide indices?
We split phrases that involve indices or powers by dividing indices. We can separate terms utilizing indices using one of two ways.
- When both bases are identical:
E.g
Whenever the bases are the same, how do you split indices?
Subtract the powers whenever dividing indices with the same base.
- Subtract the indices first
- Subtract any base number or letter coefficients
We can utilize one of the indices rules to divide indices when they are the same.
E.g.
To make the following expression easier to understand:
The base has not changed, and the indices have been subtracted.
This is the indices division law.
Example 1: There is no coefficient in front of the base.
Simplify your response and leave it in index form.
a5 ÷ a²
Subtract the indices 5 and 2.
5–2=3
So,
a5 ÷ a²=a³
Conclusion
The introduction of exponents and the law of indices were the main topics of discussion. Only the first law of indices is discussed in this article; there are two further laws of indices that are equally worth studying. The division law of indices is the second law of indices, while the law of brackets is the third. I hope that this essay aids the individual reading it in properly preparing for tests and achieving high grades.
