Simplification Questions

Implification is defined as the process of making something trivial and easy to understand and tackle .So in mathematics it is the process by virtue of which mathematical problems are made easier and understandable.

Solving questions on Simplification requires basic knowledge about the BODMAS rules . Firstly BODMAS stands for Bracket Order Division Multiplication Addition and subtraction.It is the rule that governs the basic simplification process in mathematical problems.The mnemonic is an order in which various operations are to be solved in the given problem. Moreover while solving problems related to simplifying knowledge about various squares, cubes , fractions and decimals.

To Ace the problems related to simplification command over calculations and speed is pertinent.

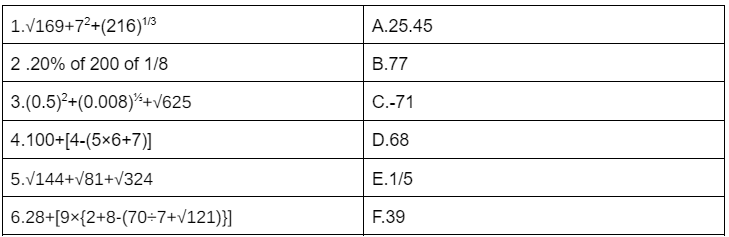
Examples 

Some of the examples of problems related to simplification are discussed below as follows -:

• {23+(17)2-(5)3+(8)3}

• In the above mentioned question as we know according to the BODMAS rule that () – round brackets precede the {} hence we first solve the curly Bracket and then round.

The solution is as follows 17×17= 289,5×5×5=125,8×8×8=512 so putting these in the order we get 

{23+(289)-(125)+(512)}={23+289-125+512}={824-125}=699

• { (65% of 3400)÷(45%of 900)}of 10%

The above-mentioned question round brackets will be solved separately followed by the curly and then the outer part.

Firstly the percentage of the numbers has to be found .65% = 65/100of 3400 = 65/100×3400= 2210 ; 45% = 45/100of 900= 45/100×900=45×9=405 .

Substituting the values we get 

{2210÷405}of 10%= 5.45×10/100=0.545

• 1/3×5/11×5/7of ?= 325

The following problem is to find the missing term .In this case we will first solve and simplify the LHS followed by transposing it to RHS to get the answer. 

So let us consider the missing term is X

1/3×5/11×5/7×X=325

25/231×X=325 

X= 325×231/25

X= 13×231

X= 3003

• 24×?2-8×7=3400

In the above problem the square of a term is missing. Similar to the previous example we will simplify the LHS and transpose it to RHS. So now let us consider the missing term as a. Hence the solution goes like This-:

24×a2-8×7=3400

24×a2-56=3400

24×a2=3400+56

24×a2=3456

a2=3456/24

a2=144

a=√144

a=12

• 41 .6% of 3500+800%of 5 +701=?3

In the above mentioned question the missing term is a cube of a given number .

First we have to find the percentage of the given number and after which we will simplify them following the BODMAS rule and then will find out the cube root to get to the final answer.

Let us consider that the missing term is a 

And the solution is as follows – :

41.6% × 3500+800% ×5+701

Here of refers to multiplication

And percentage is given by dividing it with 100 

So 41.6 /100×3500= 41.6×35= 1456

Similarly 800% of 5 = 800/100×5 = 8×5 =40 

So the final RHS will be 

1456+40+701= 2197

RHS = LHS hence 2197 = a3, a=(2197)⅓

a=13

• 23+(5-8×9)]×2

In this problem we will first solve the round brackets so we get (5-8×9)=(5-72)=-67 followed bybox brackets – hence we will add 23 +(-67) =23-67= -44 thus will be multiplied by 2 that is -44×2 = -88 which is the answer.

• 30-[23- {3+9-(8+5)}]

So this problem is of Multiple brackets the order is as follows -()-{}-[]

So the round brackets has 8+5= 13 followed by curly brackets {3+9-13} that will be addition followed by Subtraction so we get 12-13 = -1 than box brackets 23-{-1}= 23+1 =24 than finally the outer part 30 – 24 =6 

Solve the following-:

• 9+{59-6 of (√9+8)}
• 12+[3-6(7+6)]

Answer

• 9+{59-6×(3+8)}=9+{59-6×11}=9+{59-66}=9+{-7}=9-7=2
• 12+[3-6(12)]=12+[3-72]=12+[-69]=12-69=-57

• 55×5/11+68-90

In the above mentioned question the BODMAS rule will be applied . First Multiplication followed by addition and then Subtraction .

The solution goes like this 

55×5/11 = 5×5 = 25

So , 55 +68-90 = 123-90=33 which is the answer.

• {24+ ( 3-6+√121)} -19

In the above mentioned question the bracket rule is to be applied.

{ 24+(3-6+11)}-19

{24+(3-17)}-19

{24+(-14)}-19

{24-14}-19

10-19

-9 is the answer

• 455.01-1345.02÷24.99= 2×?

The above mentioned question uses the concept of LHS = RHS . Hence we will first simplify the left hand side based on the BODMAS rule followed by equating it to the right hand side and then finding out the mission term.

Here we will transpose the right hand side to left and then will find the  missing term by dividing the given result by 2.

So firstly we will take the missing term as a 

And substitute it in the equation .

455.01-1345.02÷24.99= 2×a

Now we will solve the left hand side first where in the division will be done first followed by subtraction.

455.01-53.8=a×2

400(approx )=a×2

200= a ( approx)

Conclusion 

The process of Simplification makes mathematical problems easy and fast. Simplification problems require knowledge about various operations, their rules and the order of solving. The most important and fundamental concept while solving problems related to simplification is the BODMAS rule which says nothing but the overall order that should be followed while solving any mathematical problem. The mnemonic is easy to remember and apply.

BODMAS stands for Bracket Order Division Multiplication Addition and subtraction and the order of solving is same as mentioned.Along with the rules if BODMAS other concept about exponents ,laws , fractions , decimals , percentage ,cubes , squares and cube and square root are some of the other operations that are used while solving the problems. Simplification is an essential concept in mathematics .