Having your heads spinning while seeing through is not something different when it comes to our all-rounder Mathematics where this one sucked out all our time and energy for that one step that we all go mad for. And here hope this article helps out to decrease that by applying our easy tactics to solve it in minutes.
Basically, let’s start from the basics where we need to know about that
WHAT IS A FACTORIAL?
In Mathematics, factorial is a significant capacity, which is utilized to observe the number of ways things can be sorted out or the arranged arrangement of numbers.
The notable inserting capacity of the factorial capacity was found by Daniel Bernoulli. The factorial idea is utilized in numerous numerical ideas like likelihood, stages and blends, successions and series, and so on
To put it plainly, a factorial is a capacity that duplicates a number by each number underneath it till 1. For instance, the factorial of 3 addresses the increase of numbers 3, 2, 1, for example, 3! = 3 × 2 × 1 and is equivalent to 6.
FORMULA FOR FACTORIAL
The equation to observe the factorial of a number is
n! = n × (n-1) × (n-2) × (n-3) × … .× 3 × 2 × 1
For a number n ≥ 1, the factorial portrayal as far as pi item documentation is:
From the above equations, the repeat connection for the factorial of a number is characterized as the result of the factorial number and factorial of that number short 1. It is given by 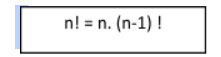
To track down the factorial of some random number, substitute the incentive for n in the above-given equation. The development of the recipe gives the numbers to be duplicated together to get the factorial of the number.
For eg.
How to find the Factorial for 8
8!= 8*7!
=8*(7*6*5*4*3*2*1)
=8*(5040)
=40,200.
FACTORIALS FOR NUMBERS
1! 1
2! 2
3! 6
4! 24
5! 120
6! 720
7! 5040
8! 40,320
9! 362,880
10! 3,628,800
11! 39,916,800
12! 479,001,600
13! 6,227,020,800
14! 8,717,8291,200
15! 1,307,674,368,000
USE OF FACTORIAL
Factorials are usually seen in the checking of permutations and pairs and in the coefficients of terms of binomial expansions. Non-integral values are used in the evaluation.
Now coming to the point, the HIGHEST POWER OF A PRIME NUMBER N DIVIDING N!
Biggest force of a prime partitioning N!
By and large, the most elevated force of an excellent p separating N! is given by
sp(N!)=⌊Np⌋+⌊Np2⌋+⌊Np3⌋+⋯
The initial term shows up since you need to count the number of terms not as much as N and are products of p and each of these contributes one p to N!. However, at that point when you have products of p2 you are not increasing only one p yet you are duplicating two of these primes p to the item. So you presently count the quantity of difference of p2 not as much as N and add them. This is caught continuously term ⌊Np2⌋. Rehash this to represent higher powers of p not as much as N.
LARGEST POWER OF A PRIME NUMBER DIVIDING WITH OTHER PRODUCTS
In general, if we need to observe the most noteworthy force of a great p separating numbers like 1×3×5×⋯×(2N−1), P(N,r), (Nr), the key is to keep in touch with them regarding factorials.
For example,
1×3×5×⋯×(2N−1)=(2N)!2NN!.
Henceforth, the biggest force of a prime, p>2, isolating 1×3×5×⋯×(2N−1) is given by sp((2N)!)−sp(N!), where sp(N!) is characterized previously. In the event that p=2, the response is sp((2N)!)−sp(N!)−N.
Likewise,
P(N,r)=N!(N−r)!.
Henceforth, the biggest force of a prime, isolating P(N,r) is given by sp(N!)−sp((N−r)!), where sp(N!) is characterized previously.
Likewise,
C(N,r)=(Nr)=N!r!(N−r)!.
Henceforth, the biggest force of a prime, isolating C(N,r) is given by
sp(N!)−sp(r!)−sp((N−r)!)
where sp(N!) is characterized previously.
AMOUNT OF ZEROS AT THE END OF N!
The quantity of zeros toward the finish of N! is given by
⌊N5⌋+⌊N52⌋+⌊N53⌋+⋯
where ⌊xy⌋ is the best number ≤xy.
To make it understood, compose N! as a result of primes N!=2α23α25α57α711α11… where αi∈N.
Note that α5<α2 at whatever point N≥2. (Why?)
The quantity of zeros toward the finish of N! is the most noteworthy force of 10 separating N!
If 10α partitions N! what’s more, since 10=2×5, 2α|N! what’s more, 5α|N!. Further, since α5<α2, the most noteworthy force of 10 separating N! is the most noteworthy force of 5 separating N! which is α5.
Note that there will be
1. A leap of 1 zero going from (N−1)! to N! if 5∥N
2. A leap of 2 zeroes going from (N−1)! to N! if 52∥N
3. A leap of 3 zeroes going from (N−1)! to N! in the event that 53∥N and overall
4. A leap of k zeroes going from (N−1)! to N! in the event that 5k∥N
where a∥b implies a partitions b and gcd(a,ba) = 1.
LEGENDRE’S FORMULA
Legendre’s recipe counts the quantity of positive numbers not exactly or equivalent to a number x which are not detachable by any of the initial a primes
Legendre’s formula counts the number of positive integers less than or equal to a number x which are not divisible by any of the first a primes,
RELATIONSHIP BETWEEN LEGENDRE’S THEOREM AND HIGHEST POWER OF A PRIME NUMBER N DIVIDING N!
The most crucial step between these two as given below
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






