Profile
Settings
Refer your friends
Sign out
In this article, we get to know about not only the diagonal of the cube formula but the face diagonal and the body diagonal of a cube. How do we use the formula, and what kind of questions can be asked related to the diagonal of the cube.
Each cube has a diagonal as the line segment connecting non-adjacent cube vertices. In geometric terms, a cube is an important shape because it has 12 equal sides and is one of the most commonly seen shapes around us. Ice cubes, sugar cubes, Rubik’s cubes, dice, etc., are examples of the cube.
Cube
All six faces of a cube are square. Cubes have identical dimensions on all their faces or sides.
There is a right angle for every plane on the Cube. A cube is a sphere where each face meets four others at each edge. An equilateral Cube has three edges and three faces at every vertex. Those surfaces on a Cube that are opposite are parallel.
In other words, a cube’s length, width, and height are of equal size, and its faces are all squares. With examples, let us learn more about how to measure the lengths of the diagonals on the face of the cube and the diagonals on the cube’s body.
Face Diagonals of a Cube and Body Diagonals of Cube:
The faces of a cube are square-shaped. Each face of the drawing has two diagonals connecting non-adjacent vertices. Therefore, there are 12 face diagonals in the cube.
In a cube, the length of each face diagonal is calculated as follows: Length of each face diagonal of a cube = √2a, where a = Length of each side.
The diagonals in the cube’s body pass through the opposite corners. Therefore, the opposite corners of a cube are connected by four body diagonals.
Derivation of Diagonal of Cube Formula
The Pythagorean theorem can be used to calculate the diagonal of a face and the internal diagonal of a cube.
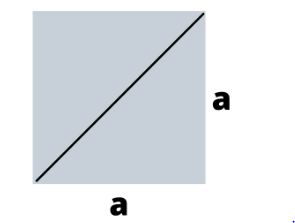
Let’s D be diagonal, and using Pythagoras theorem, we get
D² = a² + a²
D = √2a
We need to use another right triangle to find the internal diagonal. An internal diagonal is used as the hypotenuse, one side of a cube as the height, and the diagonal of a face as the base:
Using Pythagoras theorem again
D² = a² + (√2a)²
D² = a² + 2a²
D² = 3a²
D = √3a
Use of Diagonal Cube
The diagonal of a cube formula is useful for calculating the diagonal of a cube’s square faces. Using the cube’s diagonal formula, the cube’s face diagonal and main diagonal are calculated.
Each side diagonal of the cube represents a side diagonal of the cube. There are six equal faces and twelve diagonals.
As well to a square solid having all edges of the same length, a cube is a three-dimensional solid figure. In other words, the length, width, and height of a cube are equal, and each face of the cube is a square.
To calculate the dimensions of the faces and the bodies of a cube, the diagonal of a cube formula is used. As one of the seven solid figures, a cube has all its edges of the same width.
This means that the length, width, and height are of equal measure, and each of its faces is a square. Let us learn more about the diagonal of a cube and the diagonal of a cube formula for measuring the lengths of the face diagonal and the body diagonals with examples.
Example Questions on Diagonal Cube
Q.1. What is the diagonal of a cube whose side is 100 m?
Let’s be the side of the cube
The diagonal of the cube is D
Using formula
D = √3a
D = √3 ✖ 100
D = 173.2 m
So the diagonal of a cube is 173.2 m
Q.2. Calculate the length of the diagonal of a cube whose sides are 18 inches long.
Solution:
Given, the cube’s side length (a) = 18 inches,
Let the body diagonal be D
Each cube’s diagonal length = √3a
After using the formula
Length of each body diagonal of cube = √3a
⇒ √3a ⇒√3 × 18 = 31.17 inches.
Therefore, the length of the body diagonal is 31.17 inches
Conclusion
In this section, the diagonal of the cube is explained in an easy-to-understand manner. A solid cube is a three-dimensional object that contains six sides. Three edges intersect at one vertex so that there are eight vertices and 12 edges.
Moreover, we derived a formula for a cube’s diagonal, examining the differences between cubes and cuboids. The solutions given here will help you learn and understand the concepts and their applications better. This article included all the things related to the diagonal of a cube!
