Linear Equation Definition

Linear Equation is defined as an algebraic expression that can be written in the form of x+b = 0, having a variable with exponent (power) of 1. There are 2 types of the linear equation – Linear equation in one variable and linear equation in two variables. The graphical representation of a linear equation in one variable is always a straight line horizontally or vertically and the graphical representation of a linear equation in two variables is also a straight line.

What is a linear equation?

An equation with the highest exponent 1 of the variable and that equation when presented graphically, forms a straight line is called a linear equation.

Linear equation in one variable:

A linear equation in one variable is defined as an equation that is used to represent and solve for an unknown quantity. A linear equation in one variable is always in the form “ax+b=0” Where a and b are two integers and x is a variable. For example,

If x+5 = 15.

We need to find “y” from this equation i.e. only one variable is present in this equation. This equation has the highest exponent of 1 and there is only one solution of this equation. So this type of equation is known as a linear equation in one variable. Therefore, we can recognize a linear equation by seeing that only one variable is present with an exponent one on it.

Linear equation in two variables-

Linear equation in two variables is defined as an equation that is used to represent and solve for 2 unknown quantities. A linear equation in two variables is generally in the form “ax+by+c=0”. Where a, b and c are three integers, both a and b are not equal to 0 and x and y are the two variables in it.

A pair of linear equations in two variables can be solved by using different methods like the elimination method, substitution method, graphical method, and cross-multiplication method. The geometrical or graphical representation of a pair of linear equations in two variables is always a straight line. The general form of pair of linear equations in two variables are given as

p₁x + q₁y + r₁ = 0

p₂x + q₂y + r₂ = 0

In the above equations, p₁, p₂, q₁, q₂, r₁ and r₂ are the integers and p₁² + q₁² ≠ 0 and p₂² + q₂² ≠ 0. Here, p₁, p₂, q₁, q₂ are known as coefficients of the variables x and y respectively.

Linear equation formula:

There are several formulas for linear equations in one variable and linear equations in two variables where a line can be defined in an (x,y) plane. The common formulas are:-

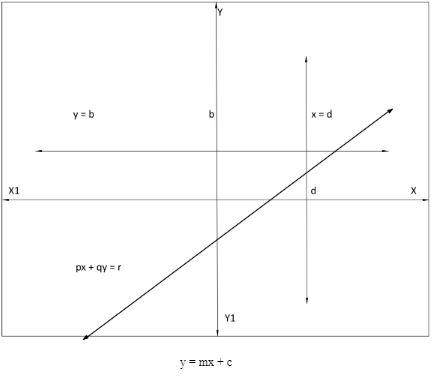
1. The linear equation formula in general standard form is written as

(px + qy = r)

Where,

• p ≠ 0
• p, q, r are real numbers
• m = -p/q

2. The linear equation formula for the vertical line is written as

x = d

3. The linear equation formula for a simple slope-intercept form is written as

(y = mx + c)

Where,

• x and y are the two variables
• m is the slope of the line and
• c is the y-intercept

The value of y when x is 0 is called the y-intercept because (0,y) is the point at which the line crosses the y-axis. Henceforth, the linear equation formula is given as: (y = mx + c)

4. The linear equation formula for the Horizontal line is written as

y = b

5. The linear equation formula for two-point form is written as

{y – y₁ )= m(x-x₁)}

Where,

• (x₁,y₁) and (x₂,y₂) are the two points on the line
• m = (y₂-y₁)/(x₂-x₁)

•     x₁≠x₂

6. The linear equation formula for intercept form is written as

x/x₀ + y/y₀ = 1

Where,

•      x₀= x-intercept
•      y₀ = y-intercept

The graphical representation of these linear equation formulas are given below