Profile
Settings
Refer your friends
Sign out
Answer: sin 37°= 3/5, sin 53°=4/5, tan 37°= 3/4, tan 53°= 4/3
To find the values, we can use complementary relations and Pythagorean triplets. Let’s proceed step by step for the process-
Let us consider a right-angled triangle with sides as a=4,b=3 and c=5 units. Here a, b, c are Pythagorean triples, which follow the relation a2+b2=c2.
As can be seen in the given figure, in this case, the angle is B= 37° or B=53°, which are also complementary angles. Complementary angles are those two angles whose sum is 90°.
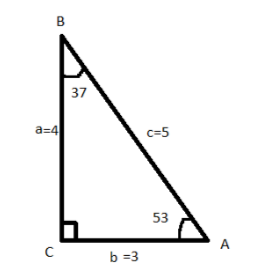
We can see that the value of base = 3 and hypotenuse = 5 for angle A. For angle B base= 4 and hypotenuse= 5
So, cos A= cos 53°= 3/5
Cos B = cos 37° = 4/5
We also know that sin (90°– A) = cos A. Therefore, cos 53° = sin 37°= 3/5 and cos 37° = sin 53° =4/5.
Now, we will move on to finding the values of tan 37° and tan 53°. We are aware of the fact that tan (angle) = perpendicular/ base.
For angle A, perpendicular = 4 and base = 3 whereas for angle B, perpendicular= 3 and base= 4. So, tan 53° = 4/3 and tan 37° = 3/4.
