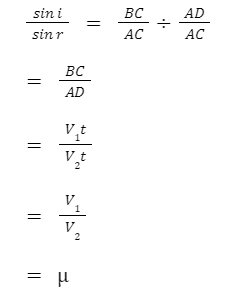Prove Laws of Reflection and Refraction Using Huygens’ principle

Huygens’ Principle is of extreme importance when studying waves and analysing them. This principle helps not only in understanding the movement of waves, but also in describing them. Electromagnetic waves can often be unpredictable and not adhere to the principles of their behaviour. Therefore, Huygens’ principle comes in extremely handy when trying to understand their behaviour regardless of the medium they are travelling in.

Waves do not move in a straight line. This movement is supported by defining characteristics possessed by waves, one of which was highlighted by Huygens in 1678. He suggested that every point on the wavefront of a wave acts as a source of a wave that is spherical in nature. This allows the waves to move freely and contributes to the peculiar behaviour of each wave. The resultant wave obtained from these spherical waves is the sum of all spherical waves.

Huygens’ Principle 

This principle is also called the Huygens-Fresnel Principle.

Huygens’ Principle states that every point on a wavefront is the source of wavelets that spread out in the forward direction at the same speed as the wave itself. 

It further elaborates on the movement of these wavelets, highlighting that they spread in all directions exactly like the primary source wave. It also mentions how at any instant of time, a tangent on any of the wavelets can give rise to a new wavefront.

The important considerations of Huygens’ Principle are:

1. All the rays, i.e., the tangents, are always perpendicular to the primary wavefront.

2. The time taken by a wave to travel from one wavefront to another will always remain constant. For a differing medium, the density may cause a change in velocity and distance, but time will remain the same.

3. All the points on a particular wavefront act like another source of spherical waves called secondary wavelets.

Huygens’ Principle and Laws of Reflection

Huygens’ Principle can be applied to prove the laws of reflection. The above figure demonstrates the incident ray being reflected by a reflecting surface. 

aA represents the wavefront incident in a reflecting mirror XY with an angle of incidence i. Every point on aA acts as a source of a secondary wavelet. As mentioned by Huygens’ principle, the rays will take equal time to cover the distance between A to D and C to B. Therefore, the angle of incidence will be equal to the angle of reflection.

This proves the first law of reflection. The direction of propagation of the secondary wavelets is also the direction of propagation of their primary wave sources.

It is also observed that the incident ray and the reflected ray lie on opposite sides of the normal. The normal is perpendicular to the reflecting surface and originates at the point of incidence. The normal, incident ray, and reflected ray lie on the same plane, and hence, the second law of reflection is proven.

Therefore, both the laws of reflection can be analysed through Huygens’ Principle.

Huygens’ Principle and Laws of Refraction

The velocity of light is changed when the light wave passes from one medium to another. This phenomenon of the bending of light is called the refraction of light. 

Let’s understand how Huygens’ Principle can help us prove the laws of refraction with the help of the above diagram. 

Considering a wavefront BC incident on the surface, we evaluate that the incident ray has a velocity of V1 and the refracted ray AD has a velocity of V2. 

Since Huygens’ Principle states that despite differences in density, the time taken by the waves to travel will be the same, let’s assume the time taken is t.

Therefore, distance BC = V1t  and AD = V2t.

Considering the triangles ABC and ADC, we get:

Here, μ is a constant. It represents the refractive index of the medium through which the light rays are travelling. Another keen observation is that the incident and refracted wavefront lie on the same plane as the normal. This proves the 2nd law of refraction.

The refractive index is also calculated as the ratio of the velocity of light in a vacuum or air to the velocity of light in another medium.

Hence, Snell’s law of refraction is proved via the application of Huygens’ Principle. This proves the first law of refraction.

Conclusion

Huygens’ Principle analyses the movement of waves across dimensions and helps us understand the unpredictability of their behaviour. Consequently, this principle is used to prove the laws of reflection and refraction of light, which are two of the most important phenomena demonstrated by light waves and attest to their behaviour as electromagnetic waves. 

The approach to proving these laws using Huygens’ Principle focuses on proving the angular observations of incident and reflected or refracted rays. The consideration of Huygens’ principle that the time taken by the light waves to travel through different media, even though it remains the same, also contributes to this analysis.